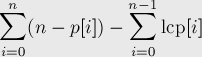Как найти i-ю подстроку строки, используя массив суффиксов и массив LCP?
Если мы организуем все отчетливый подстроки строки лексикографически и нам нужна i-я подстрока
1.) Можно ли найти его, используя массив суффиксов а также Массив LCP?
2.) Если да, как мы это делаем? это можно сделать в O (Nlog ^ N) при создании массива суффиксов с использованием Manber & Майерс, который имеет временную сложность O (Nlog ^ 2N) или при создании своего массива LCP, используя алгоритм Касая, который имеет временную сложность O (N)?
Решение
Да, это можно сделать, используя массив суффиксов и массив LCP.
Предполагая, что вы знаете, как рассчитать массив суффиксов и массив LCP.
Позволять p[] обозначить суффиксный массив lcp[] обозначим массив LCP.
создать массив, в котором будет храниться количество отдельных подстрок до i'th ранг суффикс. Это можно рассчитать по этой формуле. Для более подробной информации смотрите Вот
Позволять cum[] Обозначим совокупный массив, который можно рассчитать следующим образом:
cum[0] = n - p[0];
for i = 1 to n do:
cum[i] = cum[i-1] + (n - p[i] - lcp[i])
Теперь для поиска i'th Подстрока просто найти нижнюю границу i в совокупном массиве cum[] это даст вам ранг суффикса от того места, где должна начинаться ваша подстрока и печатать все символы до длины
i - cum[pos-1] + lcp[pos] // i lies between cum[pos-1] and cum[pos] so for finding
// length of sub string starting from cum[pos-1] we should
// subtract cum[pos-1] from i and add lcp[pos] as it is
// common string between current rank suffix and
// previous rank suffix.
где pos возвращаемое значение по нижней границе.
Весь вышеуказанный процесс может быть обобщен следующим образом:
string ithSubstring(int i){
pos = lower_bound(cum , cum + n , i);
return S.substr(arr[pos] , i - cum[pos-1] + lcp[pos]);// considering S as original character string
}
Для полной реализации массива суффиксов, LCP и выше логики вы можете увидеть Вот
Другие решения
Других решений пока нет …