Как я могу получить точку на спирали при заданных градусах вращения?

Question

Как я могу получить точку на спирали при заданных градусах вращения?

Ближайшая вещь, которую я нашел, чтобы помочь объяснить, что мне нужно, здесь в этом вопросе: Нарисуйте равноудаленные точки на спирали

Однако это не совсем то, что я хочу.

The spiral to draw is an archimedean spiral and the points obtained must be equidistant from each other. (Цитата: Из вопроса, указанного выше.)

Это именно то, что я хочу, учитывая уравнение Архимедовой Спирали, .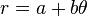

Пользователь может вводить определенный набор данных, они НЕ основаны на спиралях, а в целом на круговых фигурах. Они следующие: центральная точка [X, Y, Z], радиус, горизонтальное разделение [можно назвать разделением X, зависит от фигуры] и вертикальное разделение [можно назвать разделением Y, зависит от фигуры] и, что наиболее важно, степени вращения. Я хотел бы, чтобы горизонтальное разделение было расстоянием между последовательными точками, поскольку они должны быть на одинаковом расстоянии друг от друга. Я также хотел бы, чтобы вертикальное разделение было расстоянием между «параллельными» кривыми.

Таким образом, учитывая конкретный входной выбор (и да, некоторые могут быть проигнорированы), как я могу перебрать все последовательные эквидистантные точки, необходимые для достижения входных степеней (которые могут быть очень большими, но конечными) и вернуть X и точка Y каждой точки этих точек?

По сути, я пытаюсь достичь цикла от нуля до количества градусов на входе, учитывая все остальные входные данные и мои предпочтения, указанные выше, и рисуя точку для всех равноотстоящих последовательных точек (если Вы решаете представлять, используя код, просто представляйте рисунок, используя «печать»).

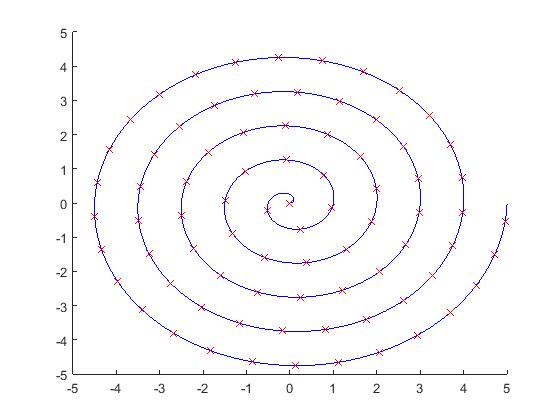
Мне трудно объяснять, но я думаю, что я довольно много об этом рассказал. Точки на этом графике именно то, что мне нужно:

-2

c++loops point spiral

Решение

Другие решения

Других решений пока нет …

Источник

Accepted Answer

Предполагая двумерный случай и архимедову спираль с центром вокруг нуля (a = 0), то есть с уравнением 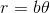$R = A \ Theta$ . Последовательные линии тогда 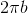$2 \ пи б$ кроме того, чтобы получить «вертикальный интервал» , задавать $б = V / (2 \ р)$ .

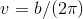Длина дуги от центра до точки под заданным углом определяется как вольфрам, но с его решением сложно работать. Вместо этого мы можем приблизить длину дуги (используя очень грубое приближение для больших тета) к 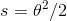s = 0.5 * theta ^ 2 .Перестановка, 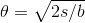S = SQRT (S / B) , что позволяет нам определить, какие углы соответствуют желаемому «горизонтальному интервалу». Если это приближение недостаточно, я бы посмотрел на что-то вроде Ньютона-Рафсона. Вопрос, на который вы ссылаетесь, также использует приближение, хотя и не то же самое.

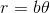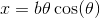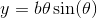Наконец, признавая, что полярные координаты $г = Ь \ тета$ перевести на декартово следующим образом: х = Ь * тета * соз (тета) ; у = Ь * тета * грех (тета) .

Я получаю следующее:

Это генерируется следующим кодом MATLAB, но он должен быть достаточно простым для перевода на C ++, если это то, что вам действительно нужно.

% Entered by user
vertspacing = 1;
horzspacing = 1;
thetamax = 10*pi;

% Calculation of (x,y) - underlying archimedean spiral.
b = vertspacing/2/pi;
theta = 0:0.01:thetamax;
x = b*theta.*cos(theta);
y = b*theta.*sin(theta);

% Calculation of equidistant (xi,yi) points on spiral.
smax = 0.5*b*thetamax.*thetamax;
s = 0:horzspacing:smax;
thetai = sqrt(2*s/b);
xi = b*thetai.*cos(thetai);
yi = b*thetai.*sin(thetai);

3