Как я могу найти самый дешевый способ в DAG, если у меня ограниченные деньги?
Таким образом, если у меня есть Направленный ациклический граф, где стоимость каждого ребра равна 0 или больше 0, если его больше 0, он будет иметь отрицательный вес (так что вы можете купить его за 5 $, и он сократит ваш путь на -20 например).
Я знаю, что мы можем легко найти самый короткий / самый дешевый способ в DAG, но что, если у нас ограниченные деньги?
Итак, представьте следующую ситуацию:
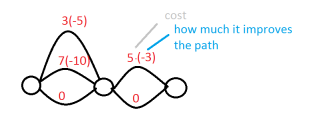
У нас есть 8 денег. Алгоритм найдет кратчайший путь, который равен -10 + -3 = -13, но это будет стоить 12, а у нас всего 8 денег, так что это не вариант. Идеальный путь будет -10 + 0, который стоит всего 7 денег.
Есть ли алгоритм, который я могу использовать для решения этой проблемы?
Решение
Эта проблема NP-Hard, с сокращением от Ранец-проблемы.
Краткое интуитивное «доказательство»: Идея состоит в том, чтобы создать вершину для каждого элемента — вы можете либо «взять», либо «не взять», выбрав вершину со стоимостью или «свободную» вершину.
Эскиз:
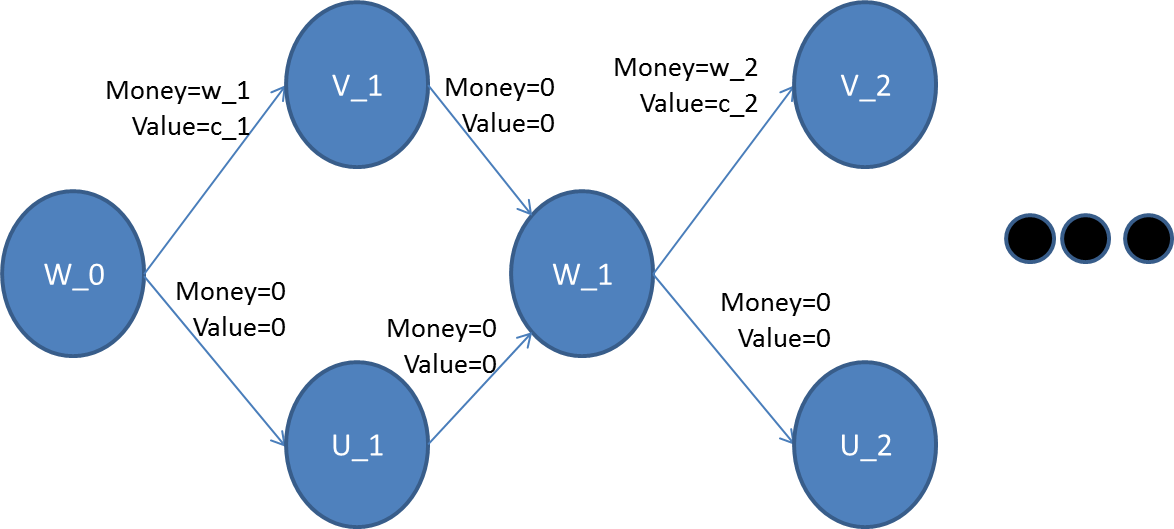
В приведенном выше примере вы видите, что из задачи о ранце создайте график, для каждого предмета вы можете взять его — и оплатить стоимость, и получить «ценность», или проигнорировать ее.
Более формально:
Учитывая случай ранца с weights=w1,w2,w3,...cn а также cost=c1,c2,..,cnс максимальным весом Wсоздать график G=(V,E) с
V= { V_i,U_i,W_i | i=0,...n }
E= { (W_i,V_i+1,U_i+1 | i=0,...,n-1} U {(V_i,W_i+1), (U_i,W_i+1) | i=0,...,n-1 }
value(W_i,V_i+1) = c_i+1
money(W_i,V_i+1) = w_i+1
value(W_i,U_i+1) = 0
money(W_i,U_i+1) = 0
money(V_i,W_i+1) = cost(V_i,W_i+1) = money(U_i,W_i+1) = cost(U_i,W_i+1) = 0
Решение этой проблемы, которое использует не более W денег, будет также решением для ранца с максимальной вместимостью W.
Возможно псевдополиномиальное решение может быть (используя Динамическое программирование техника):
D(start,0) = 0
D(v,x) = infinity x < 0
D(v,x) = min { D(u,x-money(u,v)) + value(u,v) | for each edge (u,v) } U {infinity}
В выше D(v,x) минимальное расстояние, необходимое для перемещения от начального узла до vплатя ровно x Деньги.
Обратите внимание, что это может быть сделано, потому что это DAG, так что вы можете вычислить значения от первого до последнего в соответствии с графиком топологический вид.
Когда вы закончите, вам нужно искать все значения x от 0 в MAXIMAL_AMOUNT_OF_MONEY_ALLOWED найти минимальное значение D(target,x)и это ответ.
Поиск фактической стоимости осуществляется путем возврата ваших шагов, как сделано в других решениях динамического программирования.
Время выполнения выше O(|V|*MAX_MONEY + |E|)
Другие решения
Используйте алгоритм потока. Правила:
В каждом посещенном узле обновите массив путей и их цены.
Освободите массив, когда посещаемый узел больше не нужен.
Всегда удаляйте пути с ценой> деньги.
Запустите флуд в исходном узле.
Завершение потока в целевом узле, когда все входящие ребра затоплены
Следуйте за потоком, используя исходящие края, когда все входящие края затоплены.
В конце выберите путь с самой высокой ценой в целевом узле.
Так как ваш вопрос не о поиске пути в целом, а только о поиске пути в пределах определенной стоимости, я предполагаю, что у вас уже есть некоторый алгоритм для поиска кратчайшего пути, и в целом мы поговорим о том, как его изменить.
Самый простой способ — просто игнорировать пути, которые увеличивают стоимость сверх суммы, которую вы хотите потратить. В вашем алгоритме поиска пути, когда вы добавляете ребро к пути, оставьте этот путь, если сумма затрат теперь слишком высока. Если разумно просто пропустить или пометить его как недопустимый в вашем коде, сделайте это, иначе вы можете рассматривать суммарный вес пути как бесконечность, тогда он будет обрабатывать сам себя.
Предполагая, что у вас есть какая-то функция для проверки следующего ребра вдоль пути (и если вы этого не сделаете, или нет в этом формате, просто адаптируйте его к тому, что у вас есть) …
// accepts the edge you are checking, max cost, and the sum weight and cost so far to this point
// returns float array {sum cost, sum weight), or infinity if cost is exceeded
void checkNextStep(Edge* edge, float maxCost, float* sumWeight, float* sumCost)
{
if(*sumCost + edge->cost > maxCost)
{
*sumWeight = INFINITY;
*sumCost += edge->cost;
}
*sumWeight += edge->weight;
*sumCost += edge->cost;
}
Теперь этот путь будет автоматически отклонен, если стоимость превысит ваш порог, потому что бесконечность, вероятно, не будет кратчайшим путем.
Если в итоге вы получите кратчайший путь с бесконечностью веса, это означает, что у вас недостаточно денег, чтобы добраться до вашего целевого узла по любому пути. Таким образом, вы можете использовать это в качестве проверки того, что вы вообще не можете туда добраться с помощью своей денежной системы.
