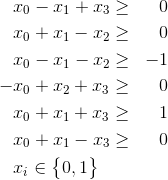Как генерировать разрезы и найти целочисленное решение
У меня есть проблема целочисленного программирования, которая выглядит, например, так, но с гораздо большим количеством переменных и ограничений
Это равносильно проблеме 3SAT. Здесь нет функции объекта, поэтому любое целочисленное решение будет оптимальным.
Теперь я могу найти нецелочисленное решение с помощью cplex и хочу добавить плоскости резки вручную. Моя проблема сейчас в том, что я не знаю точно, как создавать порезы после первого расслабления. Я нашел много работ о клике и тому подобное, но все они теоретические и не показывают алгоритм, как это сделать. Я надеюсь, что кто-то может дать мне подсказку, как произвести эти сокращения и решить это.
Решение
Ну, я вижу два основных варианта. Либо используя пользовательские сокращения или ленивые ограничения.
В обоих случаях вы можете восстановить LHS разрезов с IloExpr где переменные на разрезе могут быть добавлены с помощью += оператор, разрезы добавляются к вашему IloModel априори или апостериори, другими словами, вы можете решить добавить свои пользовательские сокращения до .solve() инструкции или сразу после нее, если вы обнаружите какой-либо нарушенный разрез. Общая конструкция строки позволяет добавлять один или даже несколько срезов одновременно, используя один из следующих двух параметров:
cplex.addCut(IloConstraint cut)
cplex.addCuts(IloConstraintArray cuts)
Предположим, что переменные, которые будут добавлены в разрез, сохраняются в IloIntArray VarInCut(env); и что вы используете IloNumVarArray x(env); или же IloIntVarArray x(env); переменные в вашей модели, вы можете построить IloConstraint cut как любое обычное ограничение в cplex-C ++ для каждой конструкции строки:
IloIntArray VarInCut(env);
IloExpr LHS;
for (int i=0; i<VarInCut.getSize(); i++) { LHS += x[VarInCut[i]]; }
Следовательно, попутно вырезать как LHS <= RHS или же LHS == RHS в случае неравенства / равенства вырезать выражение где RHS может относиться к другому IloExpr или Числовое / Целочисленное значение.
С другой стороны, Ленивые Ограничения обычно реализуются как CallBacks, которые более хитры и могут привести к более высокому риску некорректного поведения в вашем приложении, следовательно, более трудны для отладки. Взгляните на документацию CPLEX на UserCuts, LazyConstraints и пару блогов, Вот а также Вот.
Мы рады быть полезными!
Другие решения