Этот код Седжвика правильный?
Я решаю проблему оптимизации, в которой, среди прочего, я должен максимизировать потоки сетей. Я реализовал алгоритм максимизации потока на основе кода C ++, основанный на следующем код Java это появляется в книге Седжвика «Алгоритмы на Java, третье издание, часть 5: Алгоритмы графов», которая максимизирует сетевой поток, используя алгоритм PREFLOW-push на основе вершин:
class NetworkMaxFlow
{ private Network G; private int s, t;
private int[] h, wt;
private void initheights()
NetworkMaxFlow(Network G, int s, int t)
{ this.G = G; this.s = s; this.t = t;
wt = new int[G.V()]; h = new int[G.V()];
initheights();
intGQ gQ = new intGQ(G.V());
gQ.put(s); wt[t] = -(wt[s] = Edge.M*G.V());
while (!gQ.empty())
{ int v = gQ.get();
AdjList A = G.getAdjList(v);
for (Edge e = A.beg(); !A.end(); e = A.nxt())
{ int w = e.other(v), cap = e.capRto(w);
int P = cap < wt[v] ? cap : wt[v];
if (P > 0 && v == s || h[v] == h[w]+1) // first observation (see below)
{ e.addflowRto(w, P);
wt[v] -= P; wt[w] += P;
if ((w != s) && (w != t)) gQ.put(w); // enqueue w if it is not source or sink
}
}
if (v != s && v != t && wt[v] > 0) // why check v != t if t never enter the queue?
{ h[v]++; gQ.put(v); }
}
}
}
Моя реализация, основанная на этом коде, не может максимизировать следующую сеть
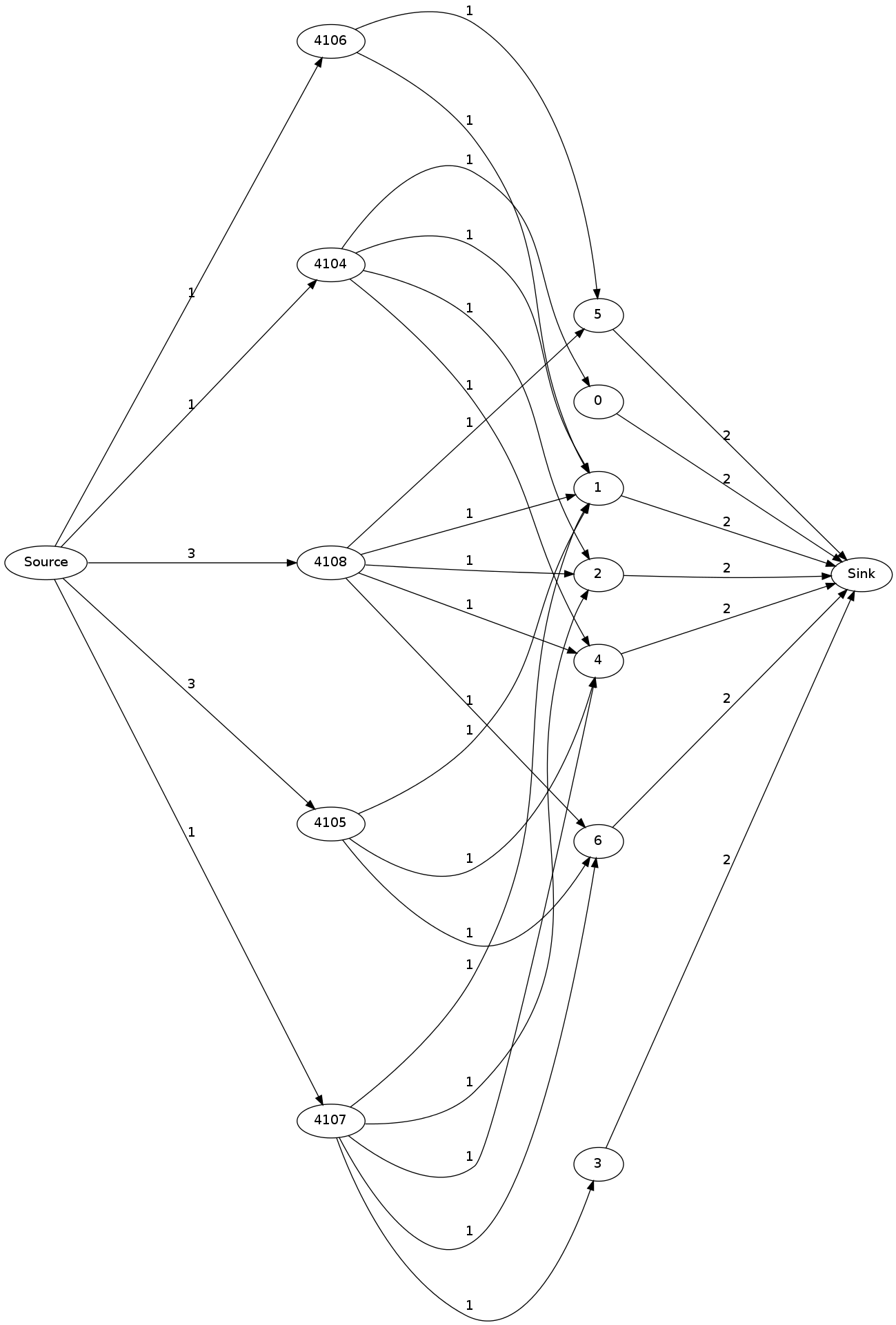
После выполнения результирующий поток выглядит следующим образом
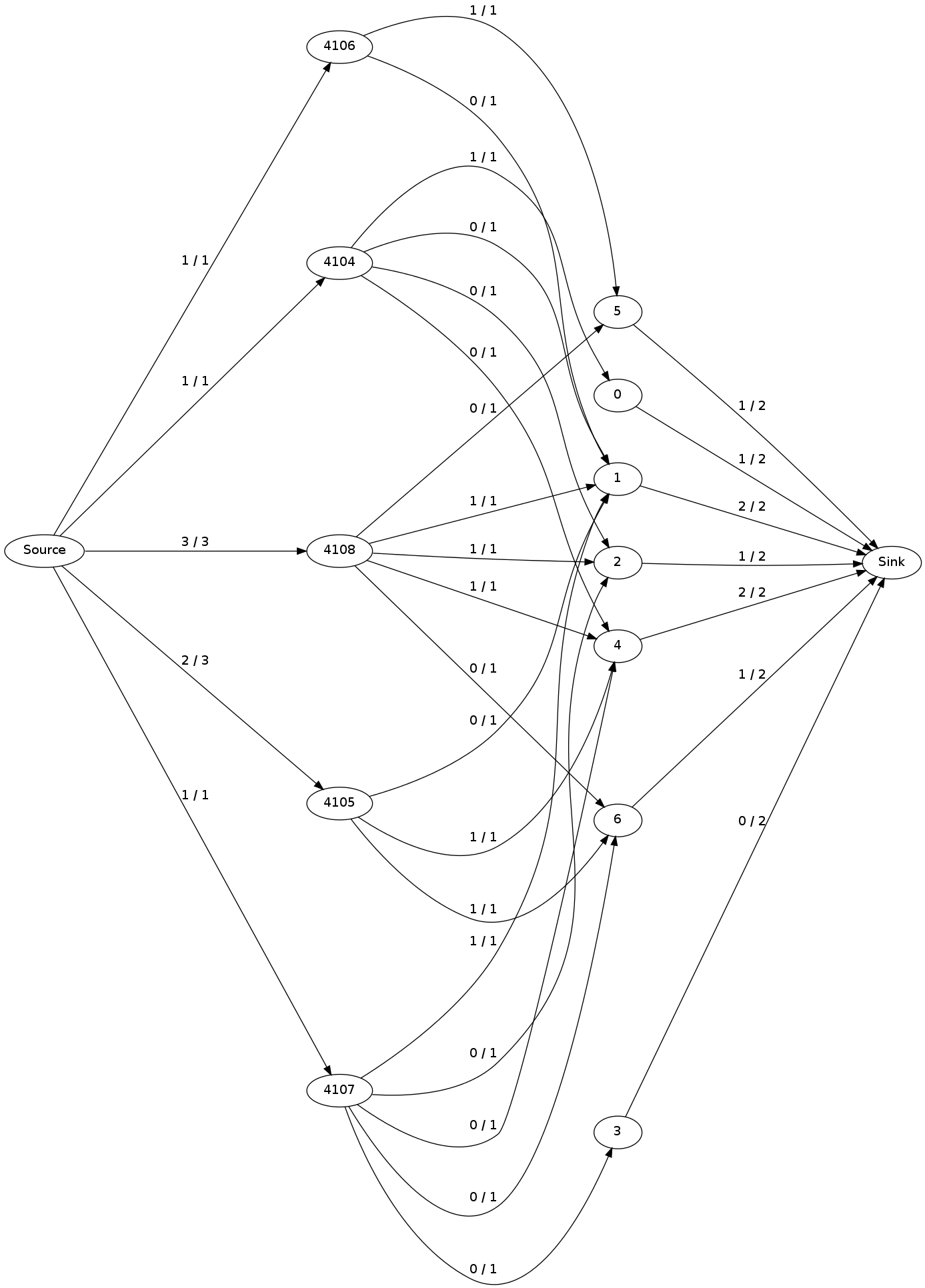
При этом расходе значение потока равно 8, но максимум равен 9, как показано на рисунке ниже.
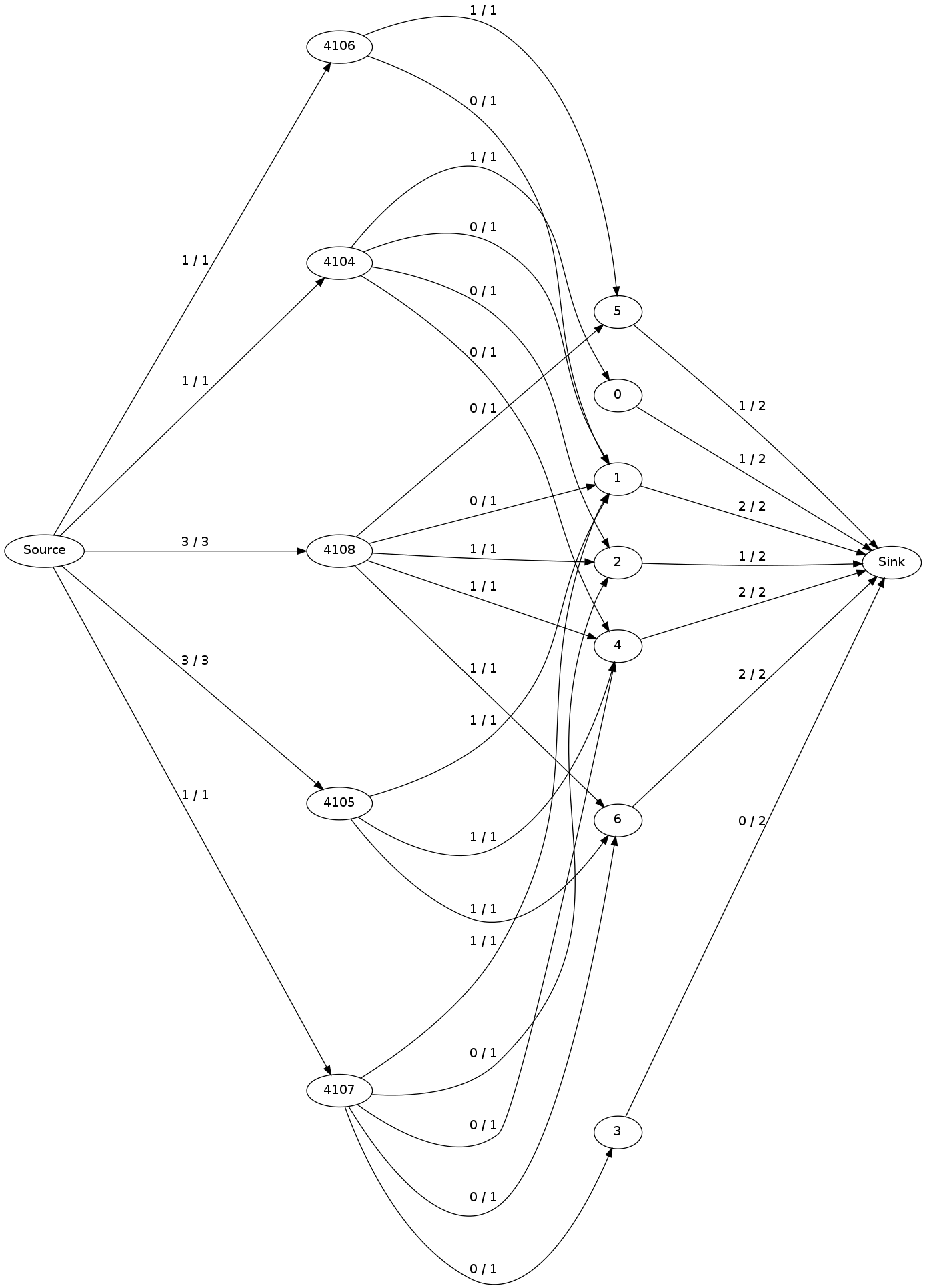
Насколько я понимаю, алгоритм согласуется с объяснением книги. Тем не менее, я вижу две странные вещи
- Нет явной фазы предварительного потока из источника. Входит в
whileи выполняется первый и только один раз, когда предикатP > 0 && v == sправда. Может быть, это было сделано, чтобы сократить код - Согласно моему пониманию и дискурсу книги, раковина никогда не входит в очередь. Однако, когда высота увеличивается, код проверяет, что v! = T. Есть причина для этого?
Это выдержка из моей реализации этого алгоритма в C ++
template <class Net, class Q_Type> typename Net::Flow_Type
generic_preflow_vertex_push_maximum_flow(Net & net)
{
init_height_in_nodes(net); // breadth first traverse from sink to
// source. Nodes are labeled with their
// minimal distance (in nodes) to sink
auto source = net.get_source();
auto sink = net.get_sink();
using Itor = __Net_Iterator<Net>;
Q_Type q; // generic queue (can be fifo, heap or random) of active nodes
// preflow: floods all nodes connected to the source
for (Itor it(source); it.has_curr(); it.next())
{
auto arc = it.get_curr();
arc->flow = arc->cap; // saturate arc to its maximum
auto tgt = net.get_tgt_node(arc);
put_in_active_queue(q, tgt);
assert(node_height<Net>(source) == node_height<Net>(tgt) + 1);
assert(not is_residual<Net>(source, arc));
}
while (not q.is_empty()) // while there are active nodes
{
auto src = get_from_active_queue(q);
auto excess = net.get_in_flow(src) - net.get_out_flow(src);
for (Itor it(src); it.has_curr(); it.next())
{
auto arc = it.get_curr();
auto tgt = net.get_connected_node(arc, src);
if (node_height<Net>(src) != node_height<Net>(tgt) + 1)
continue; // this arc is not eligible
typename Net::Flow_Type flow_to_push;
if (is_residual<Net>(src, arc))
{
flow_to_push = std::min(arc->flow, excess);
arc->flow -= flow_to_push;
}
else
{
flow_to_push = std::min(arc->cap - arc->flow, excess);
arc->flow += flow_to_push;
}
excess -= flow_to_push;
if (tgt != sink and tgt != source)
put_in_active_queue(q, tgt);
}
if (excess > 0) // src still active?
{
node_height<Net>(src)++;
put_in_active_queue(q, src);
}
}
return net.flow_value(); // sum of all outing flow from source
}
Find Кто-нибудь обнаружил какое-либо логическое несоответствие между моим кодом и кодом Седжвика? У меня сложилось впечатление, что мой код (и, возможно, также Sedgewick) неправильно обрабатывает увеличение высоты. Но мне не удается понять, почему
Я показываю подробную трассировку выполнения с сетью, которая не в состоянии максимизировать (трассировка начинается с первого q.get () из while. Значения в скобках — это значения высот. IN — входящий поток на узел. OUT — Исходящий.
Как пример, линия
4104 (2) --> 0 (1) pushing 1 from 4104 toward 0
относится к подходящей дуге 4104 -> 0. Узел 4104 имеет высоту 2, а узел 0 имеет высоту 1. Выражение «нажатие 1» означает, что 1 единица потока перемещается к целевому узлу (0). Линия ================ отделяет каждую очередь извлечения. Очередь FIFO, и ее состояние печатается в конце каждой обработки.
Обратите внимание, что во многих случаях единицы нулевого потока сдвигаются или уменьшаются, но узел назначения становится активным.
Это трассировка выполнения
Initial Queue = 4104 4105 4106 4107 4108
Active node 4104 Height = 2 IN = 1 OUT = 0
4104 (2) --> source (3) not eligible
4104 (2) --> 0 (1) pushing 1 from 4104 toward 0
4104 (2) --> 1 (1) pushing 0 from 4104 toward 1
4104 (2) --> 2 (1) pushing 0 from 4104 toward 2
4104 (2) --> 4 (1) pushing 0 from 4104 toward 4
Excess = 0
Queue = 4105 4106 4107 4108 0 1 2 4
================
Active node 4105 Height = 2 IN = 3 OUT = 0
4105 (2) --> source (3) not eligible
4105 (2) --> 1 (1) pushing 1 from 4105 toward 1
4105 (2) --> 4 (1) pushing 1 from 4105 toward 4
4105 (2) --> 6 (1) pushing 1 from 4105 toward 6
Excess = 0
Queue = 4106 4107 4108 0 1 2 4 6
================
Active node 4106 Height = 2 IN = 1 OUT = 0
4106 (2) --> source (3) not eligible
4106 (2) --> 1 (1) pushing 1 from 4106 toward 1
4106 (2) --> 5 (1) pushing 0 from 4106 toward 5
Excess = 0
Queue = 4107 4108 0 1 2 4 6 5
================
Active node 4107 Height = 2 IN = 1 OUT = 0
4107 (2) --> source (3) not eligible
4107 (2) --> 1 (1) pushing 1 from 4107 toward 1
4107 (2) --> 2 (1) pushing 0 from 4107 toward 2
4107 (2) --> 3 (1) pushing 0 from 4107 toward 3
4107 (2) --> 4 (1) pushing 0 from 4107 toward 4
4107 (2) --> 6 (1) pushing 0 from 4107 toward 6
Excess = 0
Queue = 4108 0 1 2 4 6 5 3
================
Active node 4108 Height = 2 IN = 3 OUT = 0
4108 (2) --> source (3) not eligible
4108 (2) --> 1 (1) pushing 1 from 4108 toward 1
4108 (2) --> 2 (1) pushing 1 from 4108 toward 2
4108 (2) --> 4 (1) pushing 1 from 4108 toward 4
4108 (2) --> 5 (1) pushing 0 from 4108 toward 5
4108 (2) --> 6 (1) pushing 0 from 4108 toward 6
Excess = 0
Queue = 0 1 2 4 6 5 3
================
Active node 0 Height = 1 IN = 1 OUT = 0
0 (1) --> sink (0) pushing 1 from 0 toward sink
0 (1) --> 4104 (2) not eligible
Excess = 0
Queue = 1 2 4 6 5 3
================
Active node 1 Height = 1 IN = 4 OUT = 0
1 (1) --> sink (0) pushing 2 from 1 toward sink
1 (1) --> 4105 (2) not eligible
1 (1) --> 4106 (2) not eligible
1 (1) --> 4107 (2) not eligible
1 (1) --> 4108 (2) not eligible
Excess = 2 1 goes back onto queue with label 2
Queue = 2 4 6 5 3 1
================
Active node 2 Height = 1 IN = 1 OUT = 0
2 (1) --> sink (0) pushing 1 from 2 toward sink
2 (1) --> 4108 (2) not eligible
Excess = 0
Queue = 4 6 5 3 1
================
Active node 4 Height = 1 IN = 2 OUT = 0
4 (1) --> sink (0) pushing 2 from 4 toward sink
4 (1) --> 4105 (2) not eligible
4 (1) --> 4108 (2) not eligible
Excess = 0
Queue = 6 5 3 1
================
Active node 6 Height = 1 IN = 1 OUT = 0
6 (1) --> sink (0) pushing 1 from 6 toward sink
6 (1) --> 4105 (2) not eligible
Excess = 0
Queue = 5 3 1
================
Active node 5 Height = 1 IN = 0 OUT = 0
5 (1) --> sink (0) pushing 0 from 5 toward sink
Excess = 0
Queue = 3 1
================
Active node 3 Height = 1 IN = 0 OUT = 0
3 (1) --> sink (0) pushing 0 from 3 toward sink
Excess = 0
Queue = 1
================
Active node 1 Height = 2 IN = 4 OUT = 2
1 (2) --> 4105 (2) not eligible
1 (2) --> 4106 (2) not eligible
1 (2) --> 4107 (2) not eligible
1 (2) --> 4108 (2) not eligible
Excess = 2 1 goes back onto queue with label 3
Queue = 1
================
Active node 1 Height = 3 IN = 4 OUT = 2
1 (3) --> 4105 (2) Reducing 1 from 1 toward 4105
1 (3) --> 4106 (2) Reducing 1 from 1 toward 4106
1 (3) --> 4107 (2) Reducing 0 from 1 toward 4107
1 (3) --> 4108 (2) Reducing 0 from 1 toward 4108
Excess = 0
Queue = 4105 4106 4107 4108
================
Active node 4105 Height = 2 IN = 3 OUT = 2
4105 (2) --> source (3) not eligible
4105 (2) --> 1 (3) not eligible
Excess = 1 4105 goes back onto queue with label 3
Queue = 4106 4107 4108 4105
================
Active node 4106 Height = 2 IN = 1 OUT = 0
4106 (2) --> source (3) not eligible
4106 (2) --> 1 (3) not eligible
4106 (2) --> 5 (1) pushing 1 from 4106 toward 5
Excess = 0
Queue = 4107 4108 4105 5
================
Active node 4107 Height = 2 IN = 1 OUT = 1
4107 (2) --> source (3) not eligible
4107 (2) --> 2 (1) pushing 0 from 4107 toward 2
4107 (2) --> 3 (1) pushing 0 from 4107 toward 3
4107 (2) --> 4 (1) pushing 0 from 4107 toward 4
4107 (2) --> 6 (1) pushing 0 from 4107 toward 6
Excess = 0
Queue = 4108 4105 5 2 3 4 6
================
Active node 4108 Height = 2 IN = 3 OUT = 3
4108 (2) --> source (3) not eligible
4108 (2) --> 5 (1) pushing 0 from 4108 toward 5
4108 (2) --> 6 (1) pushing 0 from 4108 toward 6
Excess = 0
Queue = 4105 5 2 3 4 6
================
Active node 4105 Height = 3 IN = 3 OUT = 2
4105 (3) --> source (3) not eligible
4105 (3) --> 1 (3) not eligible
Excess = 1 4105 goes back onto queue with label 4
Queue = 5 2 3 4 6 4105
================
Active node 5 Height = 1 IN = 1 OUT = 0
5 (1) --> sink (0) pushing 1 from 5 toward sink
5 (1) --> 4106 (2) not eligible
Excess = 0
Queue = 2 3 4 6 4105
================
Active node 2 Height = 1 IN = 1 OUT = 1
2 (1) --> sink (0) pushing 0 from 2 toward sink
2 (1) --> 4108 (2) not eligible
Excess = 0
Queue = 3 4 6 4105
================
Active node 3 Height = 1 IN = 0 OUT = 0
3 (1) --> sink (0) pushing 0 from 3 toward sink
Excess = 0
Queue = 4 6 4105
================
Active node 4 Height = 1 IN = 2 OUT = 2
4 (1) --> 4105 (4) not eligible
4 (1) --> 4108 (2) not eligible
Excess = 0
Queue = 6 4105
================
Active node 6 Height = 1 IN = 1 OUT = 1
6 (1) --> sink (0) pushing 0 from 6 toward sink
6 (1) --> 4105 (4) not eligible
Excess = 0
Queue = 4105
================
Active node 4105 Height = 4 IN = 3 OUT = 2
4105 (4) --> source (3) Reducing 1 from 4105 toward source
4105 (4) --> 1 (3) pushing 0 from 4105 toward 1
Excess = 0
Queue = 1
================
Active node 1 Height = 3 IN = 2 OUT = 2
1 (3) --> 4107 (2) Reducing 0 from 1 toward 4107
1 (3) --> 4108 (2) Reducing 0 from 1 toward 4108
Excess = 0
Queue = 4107 4108
================
Active node 4107 Height = 2 IN = 1 OUT = 1
4107 (2) --> source (3) not eligible
4107 (2) --> 2 (1) pushing 0 from 4107 toward 2
4107 (2) --> 3 (1) pushing 0 from 4107 toward 3
4107 (2) --> 4 (1) pushing 0 from 4107 toward 4
4107 (2) --> 6 (1) pushing 0 from 4107 toward 6
Excess = 0
Queue = 4108 2 3 4 6
================
Active node 4108 Height = 2 IN = 3 OUT = 3
4108 (2) --> source (3) not eligible
4108 (2) --> 5 (1) pushing 0 from 4108 toward 5
4108 (2) --> 6 (1) pushing 0 from 4108 toward 6
Excess = 0
Queue = 2 3 4 6 5
================
Active node 2 Height = 1 IN = 1 OUT = 1
2 (1) --> sink (0) pushing 0 from 2 toward sink
2 (1) --> 4108 (2) not eligible
Excess = 0
Queue = 3 4 6 5
================
Active node 3 Height = 1 IN = 0 OUT = 0
3 (1) --> sink (0) pushing 0 from 3 toward sink
Excess = 0
Queue = 4 6 5
================
Active node 4 Height = 1 IN = 2 OUT = 2
4 (1) --> 4105 (4) not eligible
4 (1) --> 4108 (2) not eligible
Excess = 0
Queue = 6 5
================
Active node 6 Height = 1 IN = 1 OUT = 1
6 (1) --> sink (0) pushing 0 from 6 toward sink
6 (1) --> 4105 (4) not eligible
Excess = 0
Queue = 5
================
Active node 5 Height = 1 IN = 1 OUT = 1
5 (1) --> sink (0) pushing 0 from 5 toward sink
5 (1) --> 4106 (2) not eligible
Excess = 0
Queue =
Решение
Ваши вопросы
предварительная подача
Там нет явной фазы предварительного потока из
source, Входит вwhileи выполняется первый и только один раз, когда предикатP > 0 && v == sявляетсяtrue, Может быть, это было сделано, чтобы сократить код
Да, я думаю, что это было сделано для сжатия кода. В связи с назначением wt[s] = Edge.M*G.V() в начале у источника достаточно «виртуального» избытка, чтобы подпитывать предварительный поток на первой итерации алгоритма. Если вы хотите сделать такой же трюк в своей реализации, вам придется раздуть excess переменная (которую вы вычисляете на лету вместо того, чтобы хранить ее в массиве, подобном Sedgewick) во время первой итерации, когда вы встречаете исходный узел. Но вам не нужно делать это таким образом, ваше явное предварительное кодирование выглядит просто отлично и, возможно, даже делает вещи более читабельными.
Я также подозреваю, что в состоянии P > 0 && v == s || h[v] == h[w]+1 неявный приоритет оператора (P > 0 && v == s) || h[v] == h[w]+1 не был предназначен. Как это написано, чек P > 0 выполняется только для исходного случая. Не проверять это в других случаях не повредит, потому что выполнение тела с P == 0 просто добавит избыток 0 к другим узлам (который ничего не делает) и излишне добавит эти другие узлы в очередь, просто для того, чтобы они немедленно снова были удалены. Я видел, что вы реализовали это так же. Это нормально, хотя небольшая трата вычислительного времени. Наверное P > 0 && (v == s || h[v] == h[w]+1) был действительно предназначен.
Раковина в очереди
Согласно моему пониманию и дискурсу книги, раковина никогда не входит в очередь. Однако, когда высота увеличивается, код проверяет, что v! = T. Есть причина для этого?
Я согласен, это странно. Единственный способ, которым приемник может войти в очередь, — это одновременно быть источником (на графике только с одним узлом и без ребер). Тем не менее, в этом случае условие v != s уже избегает бесконечного цикла, никаких дополнительных условий не требуется.
Неправильные результаты
После выполнения результирующий поток выглядит следующим образом […] С этим потоком значение потока равно 8, но максимум равен 9
Начальные высоты
Вы получаете неправильные результаты, потому что ваши начальные высоты неверны. Я не могу сравнить код инициализации Седжвика с вашим, потому что ваш пост тоже не указывает. Но из вашего лог-файла я узнаю, что вы начинаете с высоты 3 для source, Это явно против условия для высотных функций: source должен начинаться с высоты, равной количеству узлов в вашем графике, и сохранит ее в течение всего алгоритма.
В вашем случае высота source слишком близко к высоте своих соседей вниз по течению. Это заставляет соседей вниз по течению довольно скоро вернуть некоторый поток обратно к источнику, прежде чем пытаться достаточно сильно, чтобы позволить течению дальше вниз по течению. Они должны это сделать только если нет способа дать ему стечь в раковину.
Сломанный график?
Что еще беспокоит меня, так это то, что край [4104 -> 1] кажется исчезнуть. Хотя он упоминается во время обработки узла 4104, он никогда не обнаруживается во время обработки узла 1. Упоминаются все другие входящие фронты, будь то в отношении «неприемлемо», «подталкивание» или «уменьшение». Я ожидаю, что он появится как один из трех типов, как и другие. Но опять же, я не знаю, куда именно вы положили эти записи в журнал. Тем не менее, это вызывает некоторую озабоченность, и я подумал упомянуть об этом на тот случай, если у вас все еще будут проблемы после исправления ваших высот.
Другие решения
