Эффективное Тензорное Умножение
У меня есть Матрица, которая представляет собой тензор более высокого измерения, который в принципе может быть N-мерным, но каждый размер имеет одинаковый размер. Допустим, я хочу вычислить следующее:
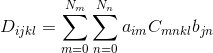
и C хранится в виде матрицы через
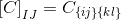
где есть некоторое отображение от ij до I и KL до J.
Я могу сделать это с помощью вложенных циклов for, где каждое измерение моего тензора имеет размер 3 через
for (int i=0; i<3; i++){
for (int j=0; j<3; j++){
I = map_ij_to_I(i,j);
for (int k=0; k<3; k++){
for (int l=0; l<3; l++){
J = map_kl_to_J(k,l);
D(I,J) = 0.;
for (int m=0; m<3; m++){
for (int n=0; n<3; n++){
M = map_mn_to_M(m,n);
D(I,J) += a(i,m)*C(M,J)*b(j,n);
}
}
}
}
}
}
но это довольно грязно и не очень эффективно. Я использую матричную библиотеку Eigen, так что я подозреваю, что, вероятно, есть гораздо лучший способ сделать это, чем цикл for или кодирование каждой записи отдельно. Я попробовал неподдерживаемую тензорную библиотеку и обнаружил, что она медленнее, чем мои явные циклы. Какие-нибудь мысли?
В качестве дополнительного вопроса, как бы я эффективно вычислил что-то вроде следующего?
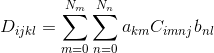
Решение
Там много работы, которую оптимизатор вашего компилятора сделает за вас. На этот раз циклы с постоянным числом итераций развернуты. Это может быть причиной того, что ваш код работает быстрее, чем библиотека.
Я бы посоветовал взглянуть на сборку, созданную с включенными оптимизациями, чтобы действительно понять, где можно оптимизировать и как на самом деле выглядит ваша программа после компиляции.
Тогда, конечно, вы можете подумать о параллельных реализациях на CPU (несколько потоков) или на GPU (cuda, OpenCL, OpenAcc и т. Д.).
Что касается бонусного вопроса, если вы подумаете о том, чтобы записать его как два вложенных цикла, я бы предложил переставить выражение так, чтобы термин a_km находился между двумя суммами. Нет необходимости выполнять это умножение во внутренней сумме, так как она не зависит от n. Хотя это, вероятно, даст лишь небольшое преимущество в производительности современных процессоров …
Другие решения
Других решений пока нет …
