Эффективно решить Ax = b, где A — симметричная метрика 4×4, а b — вектор 4×1.
Я решу небольшую линейную систему Ax = b где A это 4 на 4 симметричный матрица хранится 16 double числа (фактически 10 из них достаточно, чтобы представить это), b является вектором 4 на 1. Проблема в том, что мне приходится запускать такие системы миллион раз. Поэтому я ищу наиболее эффективную библиотеку для ее решения. Я старался cv::solve() метод в OpenCV, но я все еще нахожу это медленно.
Как матрица A симметрично, я помню Conjugate Gradient Алгоритм может быть хорошим кандидатом из-за его эффективности. Тем не менее, я еще не нашел библиотеку (у Intel MKL, кажется, есть такая, но она разработана для разреженной матрицы, плохо подходящей для моей проблемы).
Может ли кто-нибудь помочь мне с этим?
Решение
Так как размер матрицы фиксирован, я думаю, что вам лучше, если вы прямо реализуете обратное.
Существует готовая формула для этой задачи. У тебя есть:
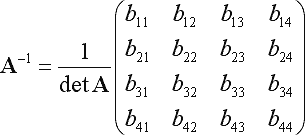
Записи B предоставляются:
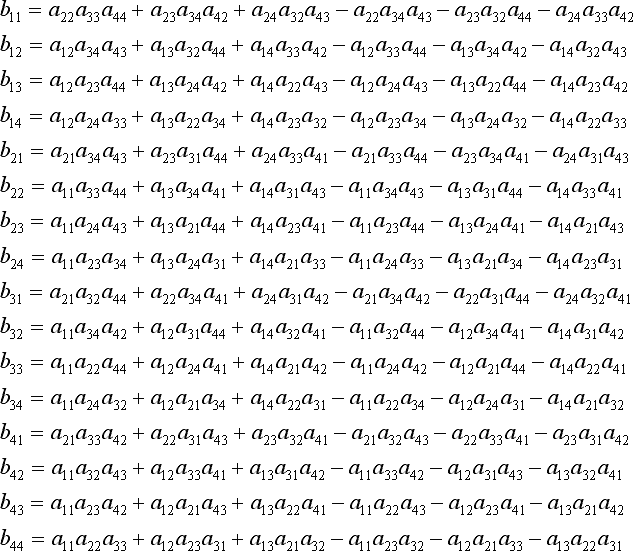
Оба формуляра взяты из этот сайт.
Вы должны быть в состоянии еще больше упростить расчет этих записей, используя тот факт, что ваша матрица симметрична. Если вы сделаете это, я думаю, вы будете быстрее, чем любая другая обратная реализация матрицы.
Тогда вам еще нужно подать заявку A^-1 на ваш b, который является простым матричным векторным умножением, вы также должны жестко кодировать, чтобы получить лучшую производительность.
Все это предполагает, что вам действительно нужна лучшая производительность для этой конкретной проблемы. Если размер матрицы изменяется или это не самая важная часть вашего алгоритма, взгляните на собственный, Lapack / Blas или любая другая библиотека линейной алгебры. Решение плотной линейной системы является фундаментальной задачей, которая должна содержаться в любой такой библиотеке.
Другие решения
Ради бога, пожалуйста, не пишите свое.
Если я правильно понимаю, вы хотите эффективно решить плотную линейную систему. Это именно то, для чего LAPACK. Версия на netlib.org (см. эта страница чтобы узнать, какую процедуру вы должны использовать) достаточно быстро, но если вам нужно что-то действительно кричащее, посмотрите на MKL, ATLAS или, возможно, GotoBLAS.
Изменить: так как это форум C ++, я должен добавить, что вы можете использовать собственный пакет, чтобы решить. Он будет использовать некоторую реализацию одной из подпрограмм LAPACK.
Тема, вероятно, устарела, но я решаю очень похожую проблему, и эта тема может быть полезна для других.
4 измерения довольно малы, поэтому эффективны алгоритмы прямого вычисления обращения матрицы. Однако, если вам нужна A-матрица только для одного решения, нет необходимости вычислять целую инверсию. Видно, что деление на определитель (операция по инверсии матрицы) необязательно для всех членов обратной матрицы. Вы можете разделить только 4 слагаемых решения вместо всех 16 матричных слагаемых. Есть и еще одна оптимизация. Вот моя реализация 4D-решателя (код C ++)
void getsub(double* sub, double* mat, double* vec)
{
*(sub++) = *(mat ) * *(mat+5) - *(mat+1) * *(mat+4);
*(sub++) = *(mat ) * *(mat+6) - *(mat+2) * *(mat+4);
*(sub++) = *(mat ) * *(mat+7) - *(mat+3) * *(mat+4);
*(sub++) = *(mat ) * *(vec+1) - *(vec ) * *(mat+4);
*(sub++) = *(mat+1) * *(mat+6) - *(mat+2) * *(mat+5);
*(sub++) = *(mat+1) * *(mat+7) - *(mat+3) * *(mat+5);
*(sub++) = *(mat+1) * *(vec+1) - *(vec ) * *(mat+5);
*(sub++) = *(mat+2) * *(mat+7) - *(mat+3) * *(mat+6);
*(sub++) = *(mat+2) * *(vec+1) - *(vec ) * *(mat+6);
*(sub ) = *(mat+3) * *(vec+1) - *(vec ) * *(mat+7);
}
void solver_4D(double* mat, double* vec)
{
double a[10], b[10]; // values of 20 specific 2D subdeterminants
getsub(&a[0], mat, vec);
getsub(&b[0], mat+8, vec+2);
*(vec++) = a[5]*b[8] + a[8]*b[5] - a[6]*b[7] - a[7]*b[6] - a[4]*b[9] - a[9]*b[4];
*(vec++) = a[1]*b[9] + a[9]*b[1] + a[3]*b[7] + a[7]*b[3] - a[2]*b[8] - a[8]*b[2];
*(vec++) = a[2]*b[6] + a[6]*b[2] - a[0]*b[9] - a[9]*b[0] - a[3]*b[5] - a[5]*b[3];
*(vec ) = a[0]*b[8] + a[8]*b[0] + a[3]*b[4] + a[4]*b[3] - a[6]*b[1] - a[1]*b[6];
register double idet = 1./(a[0]*b[7] + a[7]*b[0] + a[2]*b[4] + a[4]*b[2] - a[5]*b[1] - a[1]*b[5]);
*(vec--) *= idet;
*(vec--) *= idet;
*(vec--) *= idet;
*(vec ) *= idet;
}
*mat представить указатель на A-матрицу в виде
0 1 2 3
4 5 6 7
8 9 10 11
12 13 14 15
а также *vec представлять инерционный вектор в форме 0 1 2 3, Метод отбросить инерционный вектор и заменить его новым.
Вам нужно 74 умножения и только одно деление. Этот метод, вероятно, подходит для кодировщиков SSE (большинство операций являются двойными), если у вас есть опыт оптимизации SSE.
Этот работает хорошо для всей обратимой A-матрицы в целом. Вы можете использовать личность a[7] = b[0] для симметричной A-матрицы. Это немного, но оригинальный код для общей 4-мерной обратимой A-матрицы все еще довольно быстр.
