Эффективная идентификация подключенных ячеек \ вокселей
Я пытаюсь определить наиболее эффективный способ проверить, связаны ли две ячейки \ воксели. Я расскажу о проблеме в двух измерениях для простоты и рассмотрим ячейки на диаграмме …
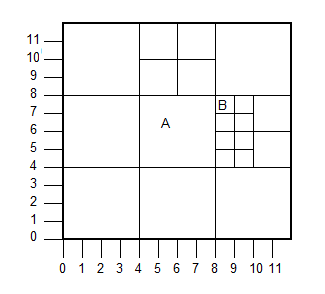
Теперь я ограничу задачу вертикальной осью, назову ее осью Y.
Нижний левый угол каждой ячейки — это ее координата, и это всегда положительное целое число (если это помогает).
Границы оси Y для A и B можно записать,
A.y1 = 4
A.y2 = 8
B.y1 = 7
B.y2 = 8
Теперь, какой самый эффективный способ проверить, соединены ли или перекрываются A и B на оси Y?
Обратите внимание, что это также должно работать, если вы поменяете метки A и B на диаграмме.
Вот моя без сомнения наивная попытка …
IF B.x2 == A.x1
IF (A.y1 <= B.y1) AND (A.y2 >= B.y2) THEN
connected = true
ELSE
IF (A.y1 >= B.y1) AND (A.y2 <= B.y2) THEN
connected = true
ELSE
connected = false
END
END
Решение
Вы можете проанализировать, как проекции ячеек на оси пересекаются друг с другом (аналогично ответу @ coproc). Но на этот раз вычислите «векторный» размер каждого пересечения, а затем проверьте, все ли они неотрицательны. Затем для проверки касания только углов вы можете запросить, чтобы хотя бы одна такая длина была положительной. Например, что-то вроде этого (для ясности я переставил структуру ограничивающего прямоугольника):
typedef int axis_t; // some signed type
struct range { axis_t low, high; };
struct box { range x, y; }
axis_t overlap(const range &a, const range &b)
{
return min(a.high, b.high) - max(a.low, b.low);
}
bool overlap(const box &a, const box &b)
{
axis_t x_overlap = overlap(a.x, b.x);
axis_t y_overlap = overlap(a.y, b.y);
return x_overlap >= 0 && y_overlap >= 0 && x_overlap + y_overlap > 0;
}
Это до 7 сравнений и 3 сложений / вычитаний, но нужно учитывать 8 значений, так что, вероятно, это не так уж и плохо.
Другие решения
Предполагая, что под связным вы подразумеваете «разделить нетривиальную границу», я подумаю об этом так: два из этих полей связаны, если они имеют две разные точки. Если вы придерживаетесь прямоугольных полей, вы просто проверяете углы каждой ячейки и смотрите, есть ли по крайней мере два из восьми углов в обоих наборах. Чтобы использовать этот подход для анализа разбиения плоскости на график, представляющий связанные поля, вы также можете использовать это, чтобы проверить, нужно ли вставлять ребро (предполагая, что это ваша конечная цель), но вам, вероятно, следует подумать о каком-либо способе сортировки их, так что вы не получите квадратично много сравнений по количеству клеток.
Только с проверками геометрии вы близки к оптимальным.
Вам нужно 4 сравнения (в 2d), чтобы определить, какая, если есть, пара ребер смежна. Если обнаружена смежность, вам необходимо обнаружить наличие или отсутствие двухмерного перекрытия. Вы делаете это с двумя проверками включения, используя <= и> =. Вы не будете делать намного лучше. Если истинные ответы более вероятны, чем ложные, возможно, стоит сначала проверить, строго ли одна конечная точка содержится в другом ребре. Если все эти тесты не пройдены, логика должна пройти окончательную проверку на идентичные ребра. (Эта дополнительная проверка делает метод более дорогим, если распространены ложные ответы.)
Эффективность доступна, если вы добавляете число «глубины» к каждому узлу. Это быстро подскажет, какая ячейка больше или имеет одинаковый размер, что позволит вам выполнить только одну из двух проверок включения. Одно сравнение глубины позволит избежать нескольких сравнений координат ребер.
Наконец, если вы поместите родительские указатели в узлы, то вы можете сделать это сравнение, ища пути до наименьшего общего предка. Эти пути могут быть проверены, чтобы получить ответ. Однако, поскольку маловероятно, что их поиск и тестирование будут быстрее, чем численное сравнение, которое у вас уже есть, я не буду вдаваться в подробности.
По мне, твой код самый лучший.
Требуется не более 6 сравнений.
Боюсь, нахождение радиуса / расстояния / перекрытия требует больше вычислений.
Один альтернативный вариант — кеширование.
Если вы кешируете соседние узлы во время хранения координат каждого блока,
позже вы можете просто посмотреть, находится ли B в соседнем списке с меньшим числом сравнений. Создание начального кеша является непроизводительной нагрузкой, но в дальнейшем производительность может быть хорошей.
Иначе лучшего пути не вижу.
