javascript — Выберите оптимальный набор образцов для аппроксимации кривой с заданным количеством образцов?
Фон
У меня есть любимый проект, который я люблю обдумывать время от времени. Проект связан с устройством ввода RC управления самолетом. Люди, знакомые с этим увлечением, вероятно, также знакомы с так называемым «экспонированием на палочке», которое является обычной особенностью RC-передатчиков, где ручки управления либо более или менее чувствительны около нейтрального центрального положения, и становятся менее или более чувствительными по мере того, как Стик приближается к своим минимальным или максимальным значениям.
Я прочитал несколько статей, которые я не до конца понимаю. У меня явно нет математического фона, чтобы решить эту проблему, поэтому я надеюсь, что, возможно, один из вас мог бы.
проблема
Я решил аппроксимировать кривую, взяв заранее определенное количество выборок и используя линейную интерполяцию, чтобы определить выходные значения для любых входных значений между точками выборки. Я пытаюсь найти способ определить наиболее оптимальный набор точек выборки.
Если вы посмотрите на этот пример типичной кривой роста для этого приложения, вы заметите, что некоторые секции являются более линейными (более прямыми), а некоторые менее линейными (более изогнутыми).
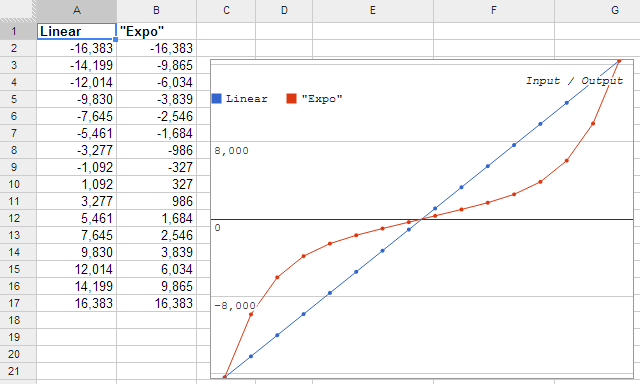
Эти образцы одинаково удалены друг от друга, но они не должны быть. Было бы разумно увеличить плотность выборки там, где есть большие изменения, и, таким образом, увеличить разрешение в извилистых сегментах, заимствуя избыточные точки из прямых сегментов.
Можно ли количественно оценить степень ошибки? Если это так, то возможно ли также определить оптимальный набор выборок для заданной функции и заранее определенное количество выборок?
Код ссылки
Фрагмент из класса, который использует предварительно рассчитанный набор точек для аппроксимации выходного значения.
/* This makes the following assumptions:
* 1. The _points[] data member contians at least 2 defined Points.
* 2. All defined Points have x and y values between MIN_VALUE and MAX_VALUE.
* 3. The Points in the array are ordered by ascending values of x.
*/
int InterpolatedCurve::value( int x ) {
if( _points[0].x >= x ) { return _points[0].y; }
for( unsigned int i = 1; i < _point_count; i++ ) {
if( _points[i].x >= x ) {
return map(x, _points[i-1].x, _points[i].x,
_points[i-1].y, _points[i].y);
}
}
// This is an error condition that is not otherwise reported.
// It won't happen as long as the points are set up correctly.
return x;
}
// Example map function (borrowed from Arduino site)
long map( long x, long x1, long x2, long y1, long y2 ) {
return (x - x1) * (y2 - y1) / (x2 - x1) + y1;
}
Хотя мой проект на самом деле написан на C ++, я использую электронную таблицу Google для получения некоторых чисел, пока размышляю над этой проблемой.
// x: Input value between -1 and 1
// s: Scaling factor for curve between 0 (linear) and 1 (maximum curve)
// c: Tunable constant
function expo_fn( x, s, c ) {
s = typeof s !== 'undefined' ? s : 1.0;
c = typeof c !== 'undefined' ? c : 4.0;
var k = c * ((c - 1.0) * s*s*s + s)/c + 1.0;
return ((k - 1.0) * x*x*x*x*x + x)/k;
};
Следующее создает набор изометрически распределенных (неоптимальных) точек между входными значениями -1 и 1. Эти выходные значения были расширены до целых чисел от -16383 до 16383 для приведенной выше электронной таблицы. Коэффициент — это значение между 0 и 1, которое определяет «кривизну» — ноль — плоская линейная кривая, а 1 — наименее линейная кривая, которую я хочу сгенерировать.
function Point( x, y ) {
this.x = x;
this.y = y;
};
function compute_points_iso( count, factor ) {
var points = [];
for( var i = 0; i < count; ++i ) {
var x = 2.0/(count - 1.0) * i - 1.0;
var y = expo_fn(x, factor);
points.push(new Point(x,y));
}
return points;
};
Соответствующая академическая работа
я учился Эта бумага описываю алгоритм выбора значимых точек данных, но моя программа пока не совсем работает. Я доложу, если получу эту штуку.
Решение
Ключевым моментом здесь является осознание того, что вы можете связать ошибку вашей линейной интерполяции в терминах второй производной функции. То есть если мы приближаемся f(x) \approx f(x_0) + f'(x_0)*(x-x_0), тогда ошибка в этом приближении меньше abs[ 0.5*f''(x_0)(x-x_0)^2 ],
Схема итеративного подхода может выглядеть следующим образом:
- Построить начальную, например, равномерно распределенный, сетка
- Вычислить вторую производную функции на этой сетке.
- Вычислить границу ошибки, используя вторую производную и интервал между выборками
- Переместите образцы ближе друг к другу, где ошибка велика; раздвиньте их дальше, где ошибка мала.
Я ожидаю, что это будет итеративное решение, которое зацикливается на шагах 2,3,4.
Большинство деталей в шаге 4.
Для фиксированного числа точек выборки можно использовать медиану границ ошибки, чтобы выбрать
где требуется более точная / грубая выборка (то есть в тех местах, где ошибка больше, чем средняя ошибка, точки выборки будут сближены).
Позволять E_0 быть этой медианой границ ошибки; тогда мы можем, для каждого образца в точке, вычислить новый желаемый интервал образца (dx')^2=2*E_0/f''(x); тогда вам понадобится некоторая логика, чтобы пройти и изменить интервал сетки так, чтобы он был ближе к этим идеальным интервалам.
На мой ответ повлияло использование алгоритма «Самоорганизующаяся карта» для данных; этот или связанные алгоритмы могут иметь отношение к вашей проблеме. Тем не менее, я не могу вспомнить когда-либо
увидеть такую проблему, как ваша, цель которой состоит в том, чтобы сделать ваши оценки ошибки равномерными по всей сетке.
Другие решения
Других решений пока нет …
