Измерение отклонения точек данных от линии; Поймать провал
(обновление: я разместил решение и код в качестве ответа, а не редактировал вопрос снова)
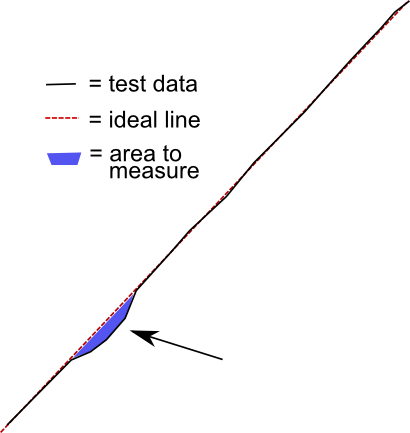
Идеальная линия (пунктирная красная линия) — это график от начальной точки со средним повышением, добавленным с каждым углом измерения; это я получаю через среднее. Я измерил данные теста черным цветом. Как я могу измерить площадь падения синим цветом? Ось X унифицирована, поэтому уклоны и математика упрощены.
Я мог бы определить отсечение по размеру таких областей, как эта, а затем пометить эту часть для повторного тестирования или неудачи. Редко бывает еще один провал, который появляется ближе к праву, но установка предельного значения для стандартного отклонения обычно не дает этих частей.
Обновить
Ответ Диего помог мне визуализировать это. Теперь, когда я вижу, что я пытаюсь сделать, я буду работать над алгоритмом для реализации «самодельного погружного детектора». 🙂
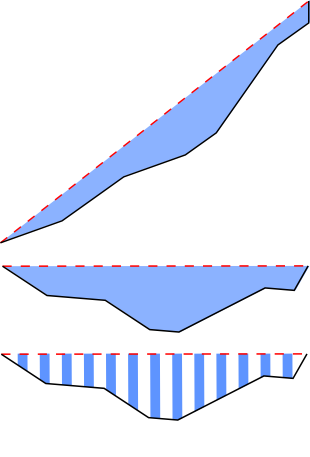
Зачем?
Я создал испытательный стенд для проверки датчиков положения дроссельной заслонки продаю. Я пытаюсь количественно определить, насколько прямолинейен график, анализируя собранные данные. Эта одна конкретная модель раздражает меня.
Пример участка, который я предпочитаю не продавать:

Ось X — это равномерно распределенные углы открытия дроссельной заслонки. Шаговый двигатель поворачивает входной вал, останавливаясь каждые 0,75 °, чтобы измерить выходной сигнал на 10-битном АЦП, который переводится в ось Y. Сюжет является переводом data[idx] в idx,value сопоставлены с (x,y) растровые координаты. Затем я рисую линии между точками внутри растрового изображения, используя алгоритм Брезенхэма.
Мои другие продукты TPS производят удивительно линейный выход.
Нижняя (левая) часть участка имеет решающее значение для нормального использования любого транспортного средства; это когда вы едете по городу, въезжаете на стоянки и т. д. Эта конкретная часть имеет тенденцию к развороту на 15 °, и я хочу использовать программу для количественной оценки этого «наклона» на кривой и меньше полагаться на интуиция тестера. В приведенном выше примере график наклоняется, но не возвращается к идеальной линии.
Несмотря на то, что это встроенное приложение, печать отчета занимает 10 секунд, поэтому я не считаю, что проходить массив из 120 точек данных несколько раз — пустая трата циклов. Кроме того, так как я использую микроконтроллер uC32 PIC32, там много памяти, поэтому я могу позволить себе эту проблему в контроллере.
Что я уже пробую
Массив подъема между контрольными точками: Я полностью отклоняю ось X, считая ее унифицированной, и затем делаю массив изменений от одного чтения к другому. Этот массив способствует тому, что в отчете «Минимальное повышение между точками: 0 Максимальное: 14». Я называю этот массив дельт.
Я пытался использовать стандартное отклонение на дельт, однако, во время тестирования я обнаружил, что низкий Std Dev не является надежной мерой для этой части. Если провал быстро возвращается к исходной линии, подразумеваемой ранними точками данных, Std Dev может быть обманчиво низким (наблюдалось, что он составляет всего 2,3), но эту часть я все еще не хотел бы использовать. Я попытался установить отсечку в 2,6, но она провалила слишком много частей с отличными графиками. Другая, более линейная часть, связанная с вышеупомянутым, может надежно рассчитывать на Std Dev по качеству.
эксцесс кажется, не подходит для этой ситуации вообще. Я узнал о эксцесс сегодня и нашел Библиотека статистики который включает в себя куртоз и асимметрию. Во время продолжительного тестирования я обнаружил, что в этих двух измерениях не было тенденции к положительному, отрицательному или амплитудному значению, которое соответствовало бы либо прохождению, либо провалу. Тот же самый джентльмен имеет библиотеку линейной регрессии, но я считаю, что Лин Рег не имеет отношения к моей ситуации, так как я согласен с предположением о AVG дельт быть моей идеальной линией. Линейная регрессия и R ^ 2 больше для нахождения линии из менее идеальных данных или гораздо больших наборов.
Сравнивая каждую дельту с AVG и Std Dev Я настроил монитор, чтобы проверить каждую дельту относительно окончательного среднего значения дельтданные. Здесь я тоже не смог найти надежную метрику. Слишком много хороших деталей не пройдет тест, ограничивающий любую дельту в пределах 2x стандартного отклонения от среднего. В конечном счете, единственное отличие от AVG, на котором я мог бы остановиться — это быть в пределах AVG+Std Dev отличие от самой AVG. Что-то более ограничительное могло бы потерпеть неудачу, иначе хорошие части. И неуловимое падение на 15 ° может пройти через этот тест.
Самодельный DIP-детектор При кормлении дельт к последовательному монитору компьютера я заметил последовательный негатив дельт во время провала, так что я запрограммировал детектор провала, но мне это кажется очень грубым. Если есть 5 или более отрицательных дельт подряд я их суммирую. Я видел, что если я возьму эту сумму отличий провала от AVG, а затем разделю на число отрицательных дельт, значение более 2,9 или 3 может означать сбой. Я наблюдал провалы продолжительностью от 6 до 15 дельт. Легко наблюдаемые провалы будут отличаться от суммы AVG до -35.
Тенденция накопленного отклонения от AVG Вышеизложенное заставило меня задуматься, наблюдая за суммированием дельт поскольку это уходит от AVG, может быть ответом. То есть я перебираю массив и суммирую отличия каждой дельты от AVG. Я думал, что был к чему-то, пока большая часть не подорвала эту теорию. Я наблюдал тенденцию изменения количества бегущих сумм от AVG менее чем 2x AVG, тем более прямая линия появилась. Многие идеальные части показывают только 8 или менее дельта-точек, где sumOfDiffs будет уходить от AVG очень далеко.
float sumOfDiffs=0.0;
for( int idx=0; idx<stop; idx++ ){
float spread = deltas[idx] - line->AdcAvgRise;
sumOfDiffs = sumOfDiffs + spread;
...
testVal = 2*line->AdcAvgRise;
if( sumOfDiffs > testVal || sumOfDiffs < -testVal ){
flag = 'S';
}
...
}
А затем появилась часть с фантастическим линейным сюжетом с 58 точками данных, где sumOfDiffs был более чем в два раза больше AVG! Я нахожу это удивительным, так как в конце ~ 120 точек данных, sumOfDiffs значение -0,000057.
Во время тестирования финал sumOfDiffs результат часто регистрируется как 0.000000, и только на очень плохих деталях он будет больше, чем .000100. На самом деле я нахожу это довольно удивительным: как «плохая часть» могла накопить большую точность.
Пример вывода из мониторинга sumOfDiffs Этот вывод ниже показывает падение. Тест наблюдает, как работает sumOfDiffs более чем в 2 раза больше AVG от AVG для всего теста. Это падение длится от дельт idx от 23 до 49; начинается с 17,25 ° и длится 19,5 °.
Avg rise: 6.75 Std dev: 2.577
idx: delta diff from avg sumOfDiffs Flag
23: 5 -1.75 -14.05 S
24: 6 -0.75 -14.80 S
25: 7 0.25 -14.55 S
26: 5 -1.75 -16.30 S
27: 3 -3.75 -20.06 S
28: 3 -3.75 -23.81 S
29: 7 0.25 -23.56 S
30: 4 -2.75 -26.31 S
31: 2 -4.75 -31.06 S
32: 8 1.25 -29.82 S
33: 6 -0.75 -30.57 S
34: 9 2.25 -28.32 S
35: 8 1.25 -27.07 S
36: 5 -1.75 -28.82 S
37: 15 8.25 -20.58 S
38: 7 0.25 -20.33 S
39: 5 -1.75 -22.08 S
40: 9 2.25 -19.83 S
41: 10 3.25 -16.58 S
42: 9 2.25 -14.34 S
43: 3 -3.75 -18.09 S
44: 6 -0.75 -18.84 S
45: 11 4.25 -14.59 S
47: 3 -3.75 -16.10 S
48: 8 1.25 -14.85 S
49: 8 1.25 -13.60 S
Final Sum of diffs: 0.000030
RunningStats analysis:
NumDataValues= 125
Mean= 6.752
StandardDeviation= 2.577
Skewness= 0.251
Kurtosis= -0.277
Отрезвляющая записка о качестве: В этом путешествии я узнал, что крупные поставщики автомобильных комплектующих считают стандартным показателем этих деталей 4-точечный тест. мой первый испытательный стенд использовал Arduino с 8 КБ ОЗУ, не имел ни TFT-дисплея, ни принтера, а механическое разрешение составляло всего 3 °! Тогда я просто проверил дельт находясь в произвольных общих пределах и выбирая предел того, насколько большой может быть любая отдельная дельта. Мой тест на 120 баллов кажется более высоким по сравнению с предыдущим тестом на 30 баллов, но этот тест не имел понятия об этих провалах.
Решение
Предпосылки
- среднее значение для набора данных имеет математическое свойство: сумма отклонений от среднего равна 0.
- это объясняет, почему как плохие, так и хорошие наборы данных всегда дают почти 0.
- в основном результат, когда отличается от нуля, по сути, представляет собой скопление ошибок округления в разностях, и поэтому, к сожалению, не может содержать полезную информацию
- то, что наиболее четко определяет то, что вы ищете, это ваш имидж: вы ищете ПЛОЩАДЬ и вот почему вы не можете найти решение таким образом:
- поиск метрики в отдельных точках слишком локальн, чтобы извлечь эту информацию
- поиск глобальных накоплений или параметров (глобальное стандартное отклонение) слишком глобален, и вы теряете данные среди слишком большого количества информации и источника вариаций
- kurtosis (вы уже сказали, что я знаю, но для полноты) выходит за рамки его применения, так как это не распределение вероятностей
- в конце концов, более подходящим подходом из ваших уже опробованных является «самодельный погружной детектор», потому что он мыслит локально, но не слишком.
- Последний, но тем не менее важный:
- Любой Алгоритм, который вы собираетесь выбрать, имеет свои молчаливые точки, на которых он стоит.
- Поэтому, возможно, кто-то ищет супер-умный алгоритм, который без параметризации и настройки автоматически адаптируется к проблеме и самостоятельно определяет результаты и другие.
- С другой стороны, есть алгоритм, который будет опираться на знание автором типичного поведения данных (хорошего и плохого) и который сам по себе глуп в том смысле, что если есть другое и непредвиденное поведение, результаты непредсказуемы.
- Хорошо, правильный путь — один из этих двух или находится между ними в зависимости от приложения. Так что, если это работает, «самодельные датчики падения» могут быть решением. Нет оснований определять его грубо, но, возможно, этого недостаточно, исходя из потребностей приложения, и это другое дело.
- Любой Алгоритм, который вы собираетесь выбрать, имеет свои молчаливые точки, на которых он стоит.
Как найти район
- Когда у вас есть данные, первым делом нужно четко определить «теоретическую прямую». Я даю несколько вариантов:
- использовать алгоритм RANSAC (формально лучший вариант ИМХО)
- это даст вам наилучшее прилегание к выровненным точкам, независимо от не выровненных
- это довольно сложно и возможно негабаритно для этой работы (ИМХО)
- рассмотрим линию, определенную первой и последней точкой
- Вы сказали, что провал почти всегда находится в одной и той же позиции, которая не находится вблизи границ, поэтому первые и последние точки можно считать доступными
- очень легко реализовать
- это пример использования знаний об ожидаемом поведении, как я говорил ранее, поэтому вам нужно подумать, насколько и насколько вы доверяете этому предположению
- рассмотрим линейное соответствие первым 10 точкам и последним 10 точкам
- Это всего лишь более доступная версия предыдущей версии, так как при использовании большего количества точек вы можете меньше беспокоиться о том, что, возможно, только первая точка или последняя были затронуты какой-либо проблемой измерения, и поэтому все терпит неудачу из-за этого
- также довольно легко реализовать
- на вашем месте я буду использовать это или что-то вдохновленное на это
- использовать алгоритм RANSAC (формально лучший вариант ИМХО)
- рассчитать значение Y, заданное прямой линией для каждого X
- рассчитать площадь между двумя кривыми (или площади под функцией
Y_dev = Y_data - Y_straightматематически то же самое) с этой процедурой:PositiveMax = 0; NegativeMax = 0;- начать с первой точки (значение может быть положительным или отрицательным) и положить во временную область аккумулятора
tmp_Area - для каждого следующего пункта
- если знак один и тот же, то накапливаем значение
- если это отличается
- перестать накапливать
- проверить, является ли накопленное значение больше, чем PositiveMax или ниже NegativeMax, и если оно больше, чем хранить как новый PositiveMax или NegativeMax
- в любом случае перезагрузите аккумулятор с
tmp_Area = Y_dev;к текущему значению, начиная таким образом, новое накопление
- в итоге у вас будут значения максимальной переоцененной смежной области и максимальной недооцененной смежной области, которые, я думаю, являются результатами, которые вы ищете.
- если вы хотите, вы можете управлять NegativeMax только на основе наблюдаемого и ожидаемого поведения данных
- Вы можете найти полезным установить порог, чтобы, если значение
Y_devниже порога вы его не накапливаете. - это для того, чтобы не получить большие скопления во многих точках, близких к прямой линии, которые могут быть похожи на накопления в нескольких точках, удаленных от линии
- необходимость этого и и надлежащий порог должны быть оценены на некоторых выборочных данных
- вам нужно найти соответствующий порог для этой смежной области, и вы можете получить его только из наблюдения выборочных данных.
- опять же: вы можете наблюдать и принимать решение о пороге, или вы можете создать хранилище хороших и плохих сэмплов и написать программу, которая автоматически узнает, какой порог использовать. Но это не алгоритм, это то, как найти его рабочие параметры, и человеческий мозг не делает ничего плохого … … это зависит только от того, ищем ли мы метод разделения плохих и хороших вещей или если мы Ищите и автоадаптивный алгоритм, который делает это .. Вы решаете цель.
Другие решения
Оказывается, результат моей интуиции, а метод Диего — это среднее от интеграла. Мне все еще не нравится это имя, поэтому я описал алгоритм и спросил на Math.SE, как это назвать, и он был перенесен в «Cross Validated», Stats.SE .
Я обновил графики после массового редактирования моего вопроса по Math.SE. Оказывается, я беру среднее из замкнутого интеграла от производной данных. : P Сначала мы собираем данные:
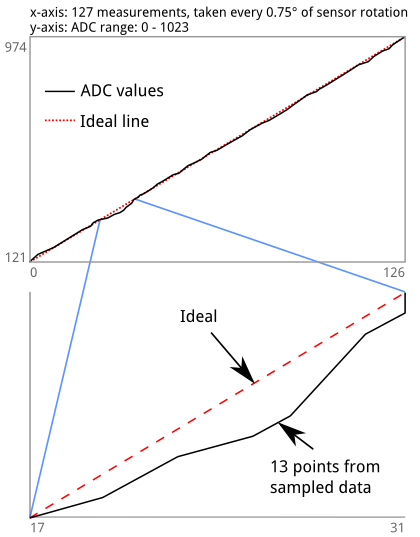
Далее идет «производная»: пошагово пройдитесь по исходному массиву данных, чтобы сформировать дельт массив, который представляет собой повышение значений АЦП от одного шага 0,75 ° до следующего. «Подъем» или «наклон» — это то, что является производной: dy / dx.
С «уклоном» или средним уровнем, я могу найти несколько отрицательных дельт подряд сложите их, затем разделите на число в конце падения. Сумма является интегралом площади между средним и дельт и когда провал становится положительным, я могу разделить сумму на количество провалов.
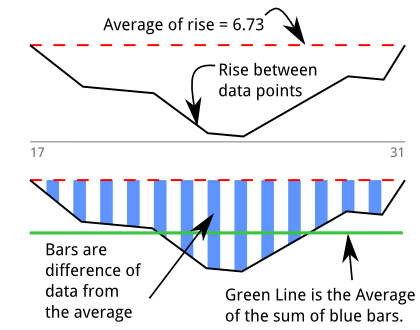
Во время тестирования я придумал значение отсечения для этого среднего значения интеграла в 2,6. Это была отличная мера моего «внутреннего инстинкта», когда я смотрел на сюжет, думая, что часть была хорошей или плохой.
На случай, если кто-то другой попытается измерить это, вот код, который я реализовал. Обратите внимание, что он ищет только отрицательные падения. Кроме того, dipCountLimit определено в другом месте как 5. В дополнение к детектору / аккумулятору провалов (т.е. числовому интегратору) у меня также есть детектор спайков, который произвольно помечает тест как плохой, если какие-либо точки данных отклоняются от среднего на величину среднего + стандартного отклонение. AVG + STD DEV в качестве предела шипа был выбран произвольно на основе наблюдаемых графиков частей, которые он потерпит неудачу.
int dipdx=0;
// inDipFlag also counts the length of this dip
int inDipFlag=0;
float dips[140] = { 0.0 };
for( int idx=0; idx<stop; idx++ ){
const float diffFromAvg = deltas[idx] - line->AdcAvgRise;
// state machine to monitor dips
const int _stop = stop-1;
if( diffFromAvg < 0 && idx < _stop ) {
// check NEXT data point for negative diff & set dipFlag to put state in dip
const float nextDiff = deltas[idx+1] - line->AdcAvgRise;
if( nextDiff < 0 && inDipFlag == 0 )
inDipFlag = 1;
// already IN a dip, and next diff is negative
if( nextDiff < 0 && inDipFlag > 0 ) {
inDipFlag++;
}
// accumulate this dip
dips[dipdx]+= diffFromAvg;
// next data point ends this dip and we advance dipdx to next dip
if( inDipFlag > 0 && nextDiff > 0 ) {
if( inDipFlag < dipCountLimit ){
// reset the accumulator, do not advance dipdx to next entry
dips[dipdx]=0.0;
} else {
// change this entry's value from dip sum to its ratio
dips[dipdx] = -dips[dipdx]/inDipFlag;
// advance dipdx to next entry
dipdx++;
}
// Next diff isn't negative, so the dip is done
inDipFlag = 0;
}
}
}
