Исходный код для расчета тригонометрических функций
Для программ, которые должны быть детерминированными и обеспечивать одинаковый результат на разных платформах (компиляторах), встроенные тригонометрические функции не могут быть использованы, поскольку алгоритм их вычисления в разных системах различен. Было проверено, что значения результата отличаются.
(Редактировать: результаты должны быть точно такими же, как в последнем бите, так как они используются в симуляции игры, которая запускается на всех клиентах. Этим клиентам необходимо, чтобы состояние симуляции было точно таким же, чтобы оно работало. Любой маленький ошибка может привести к большей и большей ошибке с течением времени, а также контроль состояния игры используется в качестве проверки синхронизации).
Таким образом, единственное решение, которое я придумал, состояло в том, чтобы использовать наш собственный пользовательский код для вычисления этих значений, проблема в том, что (удивительно) очень трудно найти какой-либо простой в использовании исходный код для всего набора тригонометрических функций.
Это моя модификация кода, который я получил (https://codereview.stackexchange.com/questions/5211/sine-function-in-c-c) для функции греха. Он является детерминированным на всех платформах, и его значение практически совпадает со значением стандартного греха (обе проверены).
#define M_1_2_PI 0.159154943091895335769 // 1 / (2 * pi)
double Math::sin(double x)
{
// Normalize the x to be in [-pi, pi]
x += M_PI;
x *= M_1_2_PI;
double notUsed;
x = modf(modf(x, ¬Used) + 1, ¬Used);
x *= M_PI * 2;
x -= M_PI;
// the algorithm works for [-pi/2, pi/2], so we change the values of x, to fit in the interval,
// while having the same value of sin(x)
if (x < -M_PI_2)
x = -M_PI - x;
else if (x > M_PI_2)
x = M_PI - x;
// useful to pre-calculate
double x2 = x*x;
double x4 = x2*x2;
// Calculate the terms
// As long as abs(x) < sqrt(6), which is 2.45, all terms will be positive.
// Values outside this range should be reduced to [-pi/2, pi/2] anyway for accuracy.
// Some care has to be given to the factorials.
// They can be pre-calculated by the compiler,
// but the value for the higher ones will exceed the storage capacity of int.
// so force the compiler to use unsigned long longs (if available) or doubles.
double t1 = x * (1.0 - x2 / (2*3));
double x5 = x * x4;
double t2 = x5 * (1.0 - x2 / (6*7)) / (1.0* 2*3*4*5);
double x9 = x5 * x4;
double t3 = x9 * (1.0 - x2 / (10*11)) / (1.0* 2*3*4*5*6*7*8*9);
double x13 = x9 * x4;
double t4 = x13 * (1.0 - x2 / (14*15)) / (1.0* 2*3*4*5*6*7*8*9*10*11*12*13);
// add some more if your accuracy requires them.
// But remember that x is smaller than 2, and the factorial grows very fast
// so I doubt that 2^17 / 17! will add anything.
// Even t4 might already be too small to matter when compared with t1.
// Sum backwards
double result = t4;
result += t3;
result += t2;
result += t1;
return result;
}
Но я не нашел ничего подходящего для других функций, таких как asin, atan, tan (кроме sin / cos) и т. Д.
Эти функции не должны быть такими точными, как стандартные, но по крайней мере 8 цифр было бы неплохо.
Решение
Я думаю, что проще всего было бы выбрать свободную библиотеку времени выполнения, которая реализует необходимые математические функции:
- FreeBSD
- идти, потребуется транслитерация, но я думаю, что все функции имеют реализацию без сборки
- MinGW-w64
- …
И просто используйте их реализации. Обратите внимание, что перечисленные выше являются либо общественным достоянием, либо лицензией BSD, либо какой-либо другой либеральной лицензией. Обязательно соблюдайте лицензии, если вы используете код.
Другие решения
«Было проверено, что значения результата отличаются».
Насколько различны достаточно разные, чтобы иметь значение? Вы утверждаете, что хотите 8 значащих (десятичных?) Цифр соглашения. Я не верю, что вы нашли меньше, чем в любой реализации, которая соответствует ИСО / МЭК 10967-3: 2006 §5.3.2.
Понимаете ли вы, как тривиометрическая ошибка составляет одну часть на миллиард? Было бы меньше 3 километров на круг размером с земную орбиту. Если вы не планируете путешествия на Марс и используете нестандартную реализацию, заявленные вами «другие» не будут иметь значения.
добавлено в ответ на комментарий:
Что каждый программист должен знать об арифметике с плавающей точкой. Прочитайте это. Шутки в сторону.
Поскольку вы утверждаете, что:
- точность не так важна, как бит для битового равенства
- вам нужно только 8 значащих цифр
тогда вы должны усечь ваши значения до 8 значащих цифр.
Вы можете использовать серию Тейлора (на самом деле кажется, что это то, что вы используете, возможно, не зная)
Взгляните на википедию (или везде):
https://en.wikipedia.org/wiki/Taylor_series
У вас есть список наиболее распространенных функций (exp, log, cos, sin и т. Д.) https://en.wikipedia.org/wiki/Taylor_series#List_of_Maclaurin_series_of_some_common_functions
но с некоторыми математическими знаниями вы можете найти / рассчитать абсолютно все (хорошо, конечно, не все, но …)
Некоторые примеры (есть много других)
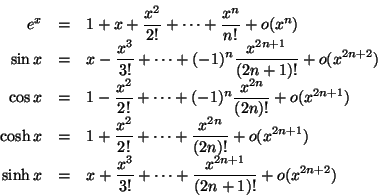
Заметки:
- чем больше терминов вы добавляете, тем больше у вас точности.
- Я не думаю, что это самый эффективный способ вычислить то, что вам нужно, но это довольно «простой» (идея, которую я имею в виду)
-
factorial(n)функция может быть очень полезна, если вы решите использовать это
Надеюсь, это поможет.
Я бы посоветовал изучить таблицы подстановки и линейную / бикубическую интерполяцию.
таким образом, вы контролируете точно значения в каждой точке, и вам не нужно выполнять очень много умножений.
Разложение по Тейлору для функций sin / cos всё равно отстой
Spring rts целую вечность боролась с такой ошибкой рассинхронизации: попробуйте опубликовать на своем форуме, осталось не так много старых разработчиков, но те, кто это сделал, должны помнить о проблемах и исправлениях.
в этой теме http://springrts.com/phpbb/viewtopic.php?f=1&т = 8265 они говорят конкретно о детерминизме libm (но разные ОС могут иметь разные libc с небольшими различиями в оптимизации, поэтому вам нужно принять подход и выбросить библиотеку)
