Хранение миллиарда полигонов в квад-дереве

Question

Хранение миллиарда полигонов в квад-дереве

Мне нужно хранить 1 миллиард пространственных многоугольников (указанных с помощью их минимальных ограничивающих прямоугольников) в квад-дереве. Для этого я написал следующий код. Однако оказывается, что для 1 миллиарда точек код выполняется очень медленно. Есть ли способ, с помощью которого я могу улучшить код, чтобы он мог работать немного быстрее. Если да, то может кто-нибудь, пожалуйста, помогите с тем же

//---------------------------------------------------------------------------
struct MBR
{
double xRight, xLeft, yBottom, yTop;
MBR *zero,*first,*second,*third;
unsigned level=0;
vector<unsigned> result; //contains the resulting intersecting spatial ids
};
bool intersects(MBR& spatialId,MBR& mbr)
{
if (mbr.yBottom > spatialId.yTop || mbr.yTop < spatialId.yBottom) return false;
if (mbr.xLeft > spatialId.xRight || mbr.xRight < spatialId.xLeft) return false;
return true;
}
//---------------------------------------------------------------------------
bool contains(MBR& spatialId,MBR& mbr)
{
if (mbr.yBottom > spatialId.yBottom || mbr.yTop < spatialId.yTop) return false;
if (mbr.xLeft > spatialId.xLeft || mbr.xRight < spatialId.xRight) return false;
return true;
}
//---------------------------------------------------------------------------
bool touches(MBR& spatialId,MBR& mbr)
{
if (    (mbr.yBottom >= spatialId.yBottom + std::numeric_limits<double>::epsilon() &&
mbr.yBottom <= spatialId.yBottom - std::numeric_limits<double>::epsilon()) ||
(mbr.yTop >= spatialId.yTop + std::numeric_limits<double>::epsilon() &&
mbr.yTop <= spatialId.yTop - std::numeric_limits<double>::epsilon()))
return true;
if (    (mbr.xLeft >= spatialId.xLeft + std::numeric_limits<double>::epsilon() &&
mbr.xLeft <= spatialId.xLeft - std::numeric_limits<double>::epsilon()) ||
(mbr.xRight >= spatialId.xRight + std::numeric_limits<double>::epsilon() &&
mbr.xRight <= spatialId.xRight - std::numeric_limits<double>::epsilon()))
return true;
return false;
}
//---------------------------------------------------------------------------
MBR MBR1,MBR2,MBR3,MBR4;
vector<unsigned> spatialIds; //contain 1 billion spatial identifiers which are intersected with MBR1, MBR2, MBR3, MBR4
//MBR1, MBR2, MBR3, MBR4 are again specified using their Minimum Bounding Rectangles
stack<MBR**> stackQuadTree;
MBR *root=new MBR();
(*root).yBottom=-90; (*root).yTop=90;
(*root).xLeft=-180; (*root).xRight=180;
(*root).level=0;
stackQuadTree.push(&root);

while(!stackQuadTree.empty())
{
MBR** node=&(*stackQuadTree.front());
if((*node)->level==50)
break;

(*node)->zero=new MBR(); (*node)->first=new MBR(); (*node)->second=new MBR(); (*node)->third=new MBR();
(*node)->zero->yBottom=(*node)->yBottom; (*node)->zero->yTop=((*node)->yBottom+(*node)->yTop)/2;
(*node)->zero->xLeft=(*node)->xLeft; (*node)->zero->xRight=((*node)->xLeft+(*node)->xRight)/2;
(*node)->zero->level=(*node)->level+1;

(*node)->first->yBottom=((*node)->yBottom+(*node)->yTop)/2; (*node)->first->yTop=(*node)->yTop;
(*node)->first->xLeft=(*node)->xLeft; (*node)->first->xRight=((*node)->xLeft+(*node)->xRight)/2;
(*node)->first->level=(*node)->level+1;

(*node)->second->yBottom=(*node)->yBottom; (*node)->second->yTop=((*node)->yBottom+(*node)->yTop)/2;
(*node)->second->xLeft=((*node)->xLeft+(*node)->xRight)/2; (*node)->second->xRight=(*node)->xRight;
(*node)->second->level=(*node)->level+1;

(*node)->third->yBottom=((*node)->yBottom+(*node)->yTop)/2; (*node)->third->yTop=(*node)->yTop;
(*node)->third->xLeft=((*node)->xLeft+(*node)->xRight)/2; (*node)->third->xRight=(*node)->xRight;
(*node)->third->level=(*node)->level+1;

MBR* node=*stackQuadTree.top();
stackQuadTree.pop();
for(vector<MBR>::iterator itSpatialId=spatialIds.begin(),lSpatialId=spatialIds.end();itSpatialId!=lSpatialId;++itSpatialId)
{
if(intersects((*itSpatialId),&(*node)->zero)||contains((*itSpatialId),&(*node)->zero)||touches((*itSpatialId),&(*node)->zero))
{
(*node)->zero->result.push_back((*itSpatialId));
stackQuadTree.push(*(*node)->zero);
}

if(intersects((*itSpatialId),&(*node)->first)||contains((*itSpatialId),&(*node)->first)||touches((*itSpatialId),&(*node)->first))
{
(*node)->first->result.push_back((*itSpatialId));
stackQuadTree.push(*(*node)->first);
}

if(intersects((*itSpatialId),&(*node)->second)||contains((*itSpatialId),&(*node)->second)||touches((*itSpatialId),&(*node)->second))
{
(*node)->second->result.push_back((*itSpatialId));
stackQuadTree.push(*(*node)->second);
}

if(intersects((*itSpatialId),&(*node)->third)||contains((*itSpatialId),&(*node)->third)||touches((*itSpatialId),&(*node)->third))
{
(*node)->third->result.push_back((*itSpatialId));
stackQuadTree.push(*(*node)->third);
}
}
}

1

c++spatial

Решение

Другие решения

log2 (1 миллиард) — приблизительно 30

Чтобы уменьшить количество операций, рассмотрите структуру данных, которая быстрее попадает в правильное соседство.

Например, если вы знаете, что ваши объекты расположены в сетке размером 10 км х 10 км, рассмотрите возможность разбиения их на сетку 10х10 (1 км х 1 км).
Затем любой объект, попадающий в определенную сетку, может сразу же перейти на 1% объектов (при условии, что они распределены равномерно).

Очевидно, что вы можете иметь рекурсивную структуру, но вам действительно не нужно больше, чем один или два 10×10 разбиения. Почему бы не попробовать верхний уровень, где каждая подсетка является квадродеревом?

Я также заметил, что у вас странная конструкция:

mbr.yTop >= spatialId.yTop + std::numeric_limits<double>::epsilon()

Я думаю, что вы можете упростить это до:

spatialId.yTop < mbr.yTop

Это своего рода определение вашего разрешения с плавающей запятой, не так ли? Если я прав, это должно значительно ускорить ваш код, но это только постоянный фактор.

class Grid {
private:
stackQuadTree qt[100]; // 10x10 array of quadtrees
public:
Grid(double xmin, double xmax, double ymin, double ymax) {
// store your 10x10 grid in the grid object
gridSizeX = 1/10 of the size of grid in the x
gridSizeY = 1/10 of the size of grid in the y
}

stackQuadTree& findGrid(MBR& mbr) {
int i = (mbr.xLeft - xmin) / gridSizeX;
int j = (mbr.yTop - ymin) / gridSizeY;
return qt[i*10+j];
}

void add(MBR& mbr) {
// add the right quadtree and add the object in
}
};

4

Ну, несколько ведет:

Вы можете ускорить свой код без изменения структуры
Вы можете ускорить ваш код, изменив структуру, чтобы стать многопоточным, и вы будете использовать несколько ядер вашего компьютера.
Лучшее решение — применить 1, а затем 2.

1)

a- sizeof(MBR) должен дать что-то вроде 76 байт + вектор dyn памяти, поэтому все объекты копируются в intersects, touches а также contains должны быть удалены. Пользы bool myfunc(const MBR & spatialId, const MBR & mbr) вместо 3-х методов, myfunc={intersects, touches , contains}.

b-
хранить std::numeric_limits<double>::epsilon() в константной переменной. Компилятору это понравится!

2)

Многопоточность процесса в основном заключается в том, чтобы парализовать внутреннюю for петля.
Простой способ сделать это — использовать OpenMP.

Попробуй окружить for цикл с #pragma директивы, что-то вроде этого:

#pragma omp parallel for
for(vector<MBR>::iterator itSpatialId=spatialIds.begin(),lSpatialId=spatialIds.end();itSpatialId!=lSpatialId;++itSpatialId)
{
// ....
}
#pragma omp barrier

но этого будет недостаточно, потому что некоторые общие данные будут доступны одновременно (что приведет к сбоям). Поэтому вы должны использовать lock / mutex / atomics для того, чтобы защитить stackQuadTree а также MBR::result на push_back«s

2

Источник

Accepted Answer

Поскольку требование состоит в том, чтобы справиться с 10⁹ записи, и даже при самом компактном представлении каждая запись составляет 16 байт (4 * sizeof(float)), нам понадобится 16 ГиБ, чтобы сохранить их в памяти. Поскольку мы хотим использовать ограничивающие прямоугольники многоугольников для индексации, каждый ограничивающий прямоугольник может принадлежать нескольким квадрантам. Если имеется много относительно больших полигонов или много перекрытий, требования к памяти для всего дерева квадрантов могут значительно возрасти. Это предполагает итеративный подход к построению дерева квадрантов, в котором мы используем файлы для хранения списков ограничивающих рамок, соответствующих каждому узлу, а также информации об узлах для всего дерева.

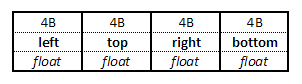
Представление прямоугольника

Мы используем прямоугольники для представления двух вещей:

Ограничительная рамка многоугольника (т.е. наши входные данные).
Ограничительная рамка квадранта (узел в дереве квадрантов).

Нам также необходимо выполнить некоторые операции с прямоугольниками, например разделить их на квадранты или определить, пересекается ли пара прямоугольников. Давайте напишем простой класс для инкапсуляции этого.

rectangle.hpp

#pragma once

#include <cstdint>

template<typename T = float>
struct rectangle_t
{
typedef typename T value_type;

rectangle_t() : left(0.0f), top(0.0f), right(0.0f), bottom(0.0f) {}
rectangle_t(value_type x1, value_type y1, value_type x2, value_type y2)
: left(x1), top(y1), right(x2), bottom(y2)
{
}

bool intersects(rectangle_t<T> const& other) const;
bool contains(rectangle_t<T> const& other) const;
bool touches(rectangle_t<T> const& other) const;
rectangle_t<T> quadrant(uint32_t n) const;

value_type left, top, right, bottom;
};

template<typename T>
inline bool rectangle_t<T>::intersects(rectangle_t<T> const& other) const
{
return !((left > other.right)
|| (right < other.left)
|| (top > other.bottom)
|| (bottom < other.top));
}

template<typename T>
inline bool rectangle_t<T>::contains(rectangle_t<T> const& other) const
{
return !((left >= other.left)
|| (right <= other.right)
|| (top >= other.top)
|| (bottom <= other.bottom));
}

template<typename T>
inline bool rectangle_t<T>::touches(rectangle_t<T> const& other) const
{
return ((left == other.right)
|| (right == other.left)
|| (top == other.bottom)
|| (bottom == other.top));
}

template<typename T>
inline rectangle_t<T> rectangle_t<T>::quadrant(uint32_t n) const
{
value_type const center_x((left + right) / 2);
value_type const center_y((top + bottom) / 2);
switch (n & 0x03) {
case 0: return rectangle_t<T>(left, top, center_x, center_y);
case 1: return rectangle_t<T>(center_x, top, right, center_y);
case 2: return rectangle_t<T>(left, center_y, center_x, bottom);
case 3: return rectangle_t<T>(center_x, center_y, right, bottom);
}
return *this; // Can't happen since we mask n
}

typedef rectangle_t<float> rectangle;

Примечание: хотя мы также предоставляем методы contains() а также touches()нам они на самом деле не нужны — если прямоугольник A содержит прямоугольник B, то оба также пересекаются. Аналогично, если два прямоугольника имеют пару ребер, которые перекрываются, они также рассматриваются как пересекающиеся.

Прямоугольная сериализация

Следующим шагом является разработка простого метода хранения прямоугольников в файле. Мы можем использовать простые двоичные файлы с макетом, который соответствует тому, как объекты представлены в памяти.

Файл содержит единственную последовательность объектов, никаких заголовков или чего-либо еще.

Поскольку мы хотим обрабатывать данные в блоках, мы реализуем простые читатель а также писатель классы, обеспечивающие эту функциональность.

rectangle_file.hpp

#pragma once

#include "rectangle.hpp"#include "config.hpp"
#include <fstream>
#include <string>
#include <vector>

typedef std::vector<rectangle> rectangle_vec;

class rectangle_writer
{
public:
rectangle_writer(std::string const& file_name);
rectangle_writer(rectangle_writer const&) = delete;

void write_block(rectangle_vec const& block);

uint64_t count() const { return count_; }

private:
std::ofstream f_;
uint64_t count_;
};

class rectangle_reader
{
public:
rectangle_reader(std::string const& file_name);
rectangle_reader(rectangle_reader const&) = delete;

void read_block(rectangle_vec& block, uint64_t n = BLOCK_SIZE);

uint64_t count() const { return count_; }
uint64_t total_count() const { return total_count_; }
uint64_t remaining_count() const { return total_count_ - count_; }

private:
std::ifstream f_;
uint64_t count_;
uint64_t total_count_;
};

rectangle_file.cpp

#include "rectangle_file.hpp"
#include <algorithm>

rectangle_writer::rectangle_writer(std::string const& file_name)
: f_(file_name, std::ios_base::binary)
, count_(0)
{
if (!f_) {
throw std::runtime_error("Unable to open index file.");
}
}

void rectangle_writer::write_block(rectangle_vec const& block)
{
f_.write(reinterpret_cast<char const*>(&block[0])
, block.size() * sizeof(rectangle));
count_ += static_cast<uint32_t>(block.size());
if (!f_) {
throw std::runtime_error("Read error.");
}
}

rectangle_reader::rectangle_reader(std::string const& file_name)
: f_(file_name, std::ios_base::binary)
, count_(0)
{
f_.seekg(0, std::ios::end);
total_count_ = static_cast<uint32_t>(f_.tellg() / sizeof(rectangle));
f_.seekg(0, std::ios::beg);
}

void rectangle_reader::read_block(rectangle_vec& block, uint64_t n)
{
uint64_t to_read(std::min(remaining_count(), n));
block.resize(to_read);
if (to_read) {
f_.read(reinterpret_cast<char*>(&block[0])
, to_read * sizeof(rectangle));
count_ += to_read;
if (!f_) {
throw std::runtime_error("Write error.");
}
}
}

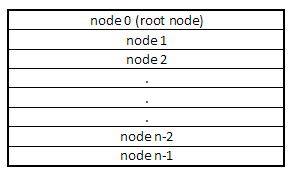
Представление Quadtree

Из-за большого количества узлов, с которыми мы, вероятно, будем работать, мы сохраняем все узлы в массиве и вместо указателей используем индексы узлов для представления иерархии. Индекс узла определяется его положением в массиве, поэтому нам не нужно его явно хранить.

Мы используем компактную структуру (node_info) для представления соответствующей информации узла:

Прямоугольник, определяющий ограничивающую рамку квадранта.
Массив из 4 индексов дочерних узлов. (Мы используем 32-битные индексы, ограничивая нас ~ 4 миллиардами узлов)

Список соответствующих прямоугольников для каждого узла хранится в файле данных, имя которого основано на индексе узла (node_XXXXXXXX.dat).

Узел легкий вес

Чтобы инкапсулировать представление quadtree и предоставить знакомый интерфейс для управления им, мы создаем класс flyweight node, держа ссылку на quadtree, индекс узла и текущий уровень в дереве (16 байт). Этот класс предоставляет всю функциональность, необходимую для построения и использования дерева квадрантов:

Чтение и запись ограничительной рамки.
Чтение и запись списков соответствующих прямоугольников.
Доступ к дочерним узлам, индекс узла, текущий уровень, …
Добавление дочерних узлов

quadtree.hpp

#pragma once

#include "rectangle.hpp"#include "rectangle_file.hpp"
#include <string>
#include <vector>

class quadtree
{
public:
class node
{
public:
rectangle& bounds();
rectangle const& bounds() const;

node child(uint32_t i) const;

rectangle_reader reader() const;
rectangle_writer writer() const;

std::string rectangle_file_name() const;

void add_child_nodes() const;

bool is_leaf_node() const;

uint32_t index() const;
uint32_t level() const;

private:
friend class quadtree;
node(quadtree& tree, uint32_t index, uint32_t level);

quadtree& tree_;
uint32_t index_;
uint32_t level_;
};

public:
enum {
ROOT_NODE_INDEX = 0
, QUADRANT_COUNT = 4
};

quadtree(quadtree&& other);
~quadtree();

static quadtree create(std::string const& dir_name
, rectangle const& bounds);
static quadtree load(std::string const& dir_name);

void save();

node get_node(uint32_t i = ROOT_NODE_INDEX);
uint32_t node_count() const;

private:
quadtree(std::string const& dir_name);
std::string index_file_name() const;

uint32_t add_node(rectangle const& bounds);
void add_child_nodes(uint32_t n);

private:
struct node_info
{
node_info();
explicit node_info(rectangle const& bounds);

rectangle bounds;
uint32_t child[4];
};
typedef std::vector<node_info> node_list;

std::string dir_name_;
node_list nodes_;
};

inline quadtree::node::node(quadtree& tree, uint32_t index, uint32_t level)
: tree_(tree)
, index_(index)
, level_(level)
{
}

inline rectangle& quadtree::node::bounds()
{
return tree_.nodes_[index_].bounds;
}

inline rectangle const& quadtree::node::bounds() const
{
return tree_.nodes_[index_].bounds;
}

inline quadtree::node quadtree::node::child(uint32_t i) const
{
return node(tree_, tree_.nodes_[index_].child[i], level_ + 1);
}

inline bool quadtree::node::is_leaf_node() const
{
return !((tree_.nodes_[index_].child[0])
|| (tree_.nodes_[index_].child[1])
|| (tree_.nodes_[index_].child[2])
|| (tree_.nodes_[index_].child[3]));
}

inline uint32_t quadtree::node::index() const
{
return index_;
}

inline uint32_t quadtree::node::level() const
{
return level_;
}

Quadtree Serialization

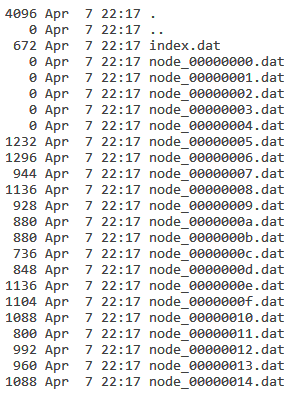
Расположение на диске снова соответствует тому, как объекты представлены в памяти.

Файл узла — это простой двоичный файл, содержащий одну последовательность объектов:

Для иллюстрации, вот как на диске появляется трехуровневое дерево (корень + 2 уровня потомков) с 1000 прямоугольниками:

конфигурация

config.hpp

#pragma once

#define BLOCK_SIZE (1024 * 8)

#define QUADTREE_LOGGING 0
#define WORKQUEUE_LOGGING 0
#define PROGRESS_LOGGING 1

Мы основываем нашу обработку на следующих наблюдениях:

Дерево только с корневым узлом все еще является допустимым деревом.
Мы можем подразделить любое допустимое дерево, чтобы получить более глубокое дерево с более подробной категоризацией.

Инициализация Quadtree

Начальный шаг — создать простейшее допустимое дерево квадрантов: только с корневым узлом, содержащим все ограничивающие рамки.

Поскольку у меня не было данных, которые я мог бы использовать, я написал простой генератор, который создает настраиваемое количество случайных прямоугольников и использует их для инициализации дерева.

gen_rnd_tree.cpp

#include "rectangle.hpp"#include "rectangle_file.hpp"#include "quadtree.hpp"#include "config.hpp"
#include <algorithm>
#include <cstdint>
#include <chrono>
#include <iostream>
#include <random>
#include <vector>

#if defined(_WIN32)
#include <direct.h>
#endif

void generate_random(uint32_t n, quadtree& qt)
{
rectangle_writer writer(qt.get_node().writer());

std::vector<rectangle> buffer;
buffer.reserve(BLOCK_SIZE);

std::random_device rd;
std::mt19937 gen(rd());
std::uniform_real_distribution<rectangle::value_type> dis_x(-179.5f, 179.5f);
std::uniform_real_distribution<rectangle::value_type> dis_y(-89.5f, 89.5f);
std::exponential_distribution<rectangle::value_type> dis_wh(1.0f);

for (uint32_t i(0); i < n; ++i) {
rectangle::value_type x(dis_x(gen));
rectangle::value_type y(dis_y(gen));
rectangle::value_type half_w(std::min(dis_wh(gen), 10.0f) * 0.05f);
rectangle::value_type half_h(std::min(dis_wh(gen), 10.0f) * 0.05f);
buffer.emplace_back(x - half_w, y - half_h, x + half_w, y + half_h);

if (buffer.size() >= BLOCK_SIZE) {
writer.write_block(buffer);
buffer.clear();
#if(PROGRESS_LOGGING)
std::cout << ".";
#endif
}
}

if (!buffer.empty()) {
writer.write_block(buffer);
}
#if(PROGRESS_LOGGING)
std::cout << ".\n";
#endif
}

int main(int argc, char* argv[])
{
using std::chrono::high_resolution_clock;
using std::chrono::duration_cast;
using std::chrono::microseconds;

if (argc != 2) return -1;

std::string const TREE_DIR("tree");

#if defined(_WIN32)
_mkdir(TREE_DIR.c_str());
#else
mkdir(TREE_DIR.c_str(), 0777);
#endif

uint32_t const N_POLYGONS(atoi(argv[1]));

std::cout << "Polygon count = " << N_POLYGONS << "\n";
std::cout << "Polygon size = " << sizeof(rectangle) << " B\n";
std::cout << "Total size = " << N_POLYGONS * sizeof(rectangle) << " B\n";

std::cout << "\nGenerating...\n";

high_resolution_clock::time_point t1 = high_resolution_clock::now();

quadtree qt(quadtree::create("tree", rectangle(-180,-90,180,90)));

generate_random(N_POLYGONS, qt);

high_resolution_clock::time_point t2 = high_resolution_clock::now();

std::cout << "\n";

double dt1_us(static_cast<double>(duration_cast<microseconds>(t2 - t1).count()));
std::cout << "Generate: " << (dt1_us / 1000.0) << " ms\n";
std::cout << "\nDone.\n\n";
return 0;
}

Quadtree Subdivision

функция subdivide(quadtree& qt,...) выполняет обход дерева в глубину, используя стек. Мы могли бы сделать обход в ширину с очередью, но очередь станет очень большой, как только мы доберемся достаточно глубоко в дереве.

Мы неоднократно потребляем узлы с вершины стека, пытаемся подразделить их и помещаем их дочерние узлы в стек.

функция subdivide(quadtree::node const& qtn, ...) принимает решение о подразделении данного узла и подготавливает параметры для copy_elements(...), Когда узел разделен и все соответствующие прямоугольники перемещены на дочерние узлы, мы очищаем файл прямоугольника для данного узла.

функция copy_elements(...) читает список совпадающих прямоугольников из родительского узла и копирует их во все дочерние узлы, чьи ограничивающие рамки они пересекают.

#include "rectangle.hpp"#include "rectangle_file.hpp"#include "quadtree.hpp"
#include <algorithm>
#include <cstdint>
#include <chrono>
#include <iostream>
#include <stack>

using std::chrono::high_resolution_clock;
using std::chrono::duration_cast;
using std::chrono::microseconds;

void copy_elements(rectangle_reader& reader, quadtree::node child_node[4])
{
rectangle target[quadtree::QUADRANT_COUNT] {
child_node[0].bounds()
, child_node[1].bounds()
, child_node[2].bounds()
, child_node[3].bounds()
};

rectangle_writer writer[quadtree::QUADRANT_COUNT] {
child_node[0].writer()
, child_node[1].writer()
, child_node[2].writer()
, child_node[3].writer()
};

rectangle_vec buffer_in;
buffer_in.reserve(BLOCK_SIZE);
rectangle_vec buffer_out[quadtree::QUADRANT_COUNT];
for (auto& buffer : buffer_out) {
buffer.reserve(BLOCK_SIZE);
}

#if(PROGRESS_LOGGING)
for (; reader.remaining_count(); std::cout << ".") {
#else
for (; reader.remaining_count();) {
#endif
reader.read_block(buffer_in, BLOCK_SIZE);

for (auto const& rect : buffer_in) {
for (uint32_t i(0); i < quadtree::QUADRANT_COUNT; ++i) {
if (target[i].intersects(rect)) {
buffer_out[i].push_back(rect);
}
}
}

for (uint32_t i(0); i < quadtree::QUADRANT_COUNT; ++i) {
if (!buffer_out[i].empty()) {
writer[i].write_block(buffer_out[i]);
buffer_out[i].clear();
}
}
}
}

// Return true if we should subdivide further, false otherwise
bool subdivide(quadtree::node const& qtn, uint32_t max_depth, uint32_t max_leaf_size)
{
bool at_max_depth(qtn.level() >= max_depth);
std::cout << (at_max_depth ? "Skipping" : "Subdividing")
<< " node #" << qtn.index() << " @ level " << qtn.level() << ".\n";
if (at_max_depth) {
return false;
} else {
// Make sure reader goes out of scope before writer is created.
rectangle_reader reader(qtn.reader());
if (qtn.is_leaf_node()) {
if (reader.total_count() <= max_leaf_size) {
std::cout << "Leaf node (" << reader.total_count() << ").\n";
return false;
}
qtn.add_child_nodes();
} else if (!reader.total_count()) {
std::cout << "Branch node.\n";
return (qtn.level() < max_depth);
}

quadtree::node child_nodes[4] {
qtn.child(0)
, qtn.child(1)
, qtn.child(2)
, qtn.child(3)
};

high_resolution_clock::time_point t1(high_resolution_clock::now());

copy_elements(reader, child_nodes);

high_resolution_clock::time_point t2(high_resolution_clock::now());
double dt_us(static_cast<double>(duration_cast<microseconds>(t2 - t1).count()));

std::cout << ". (" << reader.count() << ") " << (dt_us / 1000.0) << " ms\n";
}

rectangle_writer writer(qtn.writer()); // Clean the file

std::cout << "Branch node.\n";
return (qtn.level() < max_depth);
}

void subdivide(quadtree& qt, uint32_t max_depth, uint32_t max_leaf_size)
{
std::stack<quadtree::node> work;
work.emplace(qt.get_node());
std::size_t max_queue_size(work.size());

for (; !work.empty();) {
quadtree::node node(work.top());
work.pop();

if (subdivide(node, max_depth, max_leaf_size)) {
for (uint32_t i(0); i < quadtree::QUADRANT_COUNT; ++i) {
work.emplace(node.child(i));
}
}
max_queue_size = std::max(max_queue_size, work.size());
#if(WORKQUEUE_LOGGING)
std::cout << "* Work queue " << work.size() << " (" << max_queue_size << ").\n";
#endif
}
}

int main(int argc, char* argv[])
{
uint32_t const MAX_DEPTH(atoi((argc >= 2) ? argv[1] : "2"));
uint32_t const MAX_LEAF_SIZE(atoi((argc >= 3) ? argv[2] : "100"));

std::cout << "Loading...\n";

high_resolution_clock::time_point t1(high_resolution_clock::now());

quadtree qt(quadtree::load("tree"));

if (qt.node_count() < 1) {
std::cerr << "Invalid tree.\n";
return -1;
}

std::cout << "Building tree (max_depth=" << MAX_DEPTH
<< ", max_leaf_size=" << MAX_LEAF_SIZE << ")...\n";

high_resolution_clock::time_point t2(high_resolution_clock::now());

subdivide(qt, MAX_DEPTH, MAX_LEAF_SIZE);

high_resolution_clock::time_point t3(high_resolution_clock::now());

std::cout << "\n";

std::cout << "Tree completed (" << qt.node_count() << " nodes).\n\n";

double dt1_us(static_cast<double>(duration_cast<microseconds>(t2 - t1).count()));
double dt2_us(static_cast<double>(duration_cast<microseconds>(t3 - t2).count()));
std::cout << "Load: " << (dt1_us / 1000.0) << " ms\n";
std::cout << "Process: " << (dt2_us / 1000.0) << " ms\n";
std::cout << "\nDone.\n\n";
return 0;
}

gen_rnd_tree <count> — Создать дерево с подсчитывать прямоугольники в корневом узле.
build_tree <max_depth> <max_node_size> — Разделить узлы с более чем max_node_size прямоугольники до глубины Максимальная глубина (корень на глубине 0).

Пример вывода

Polygon count = 1000
Polygon size = 16 B
Total size = 16000 B

Generating...
.

Generate: 0 ms

Done.

Loading...
Building tree (max_depth=5, max_leaf_size=100)...
Subdividing node #0 @ level 0.
.. (1000) 15.624 ms
Branch node.
Subdividing node #4 @ level 1.
.. (288) 15.625 ms
Branch node.
Subdividing node #8 @ level 2.
Leaf node (71).
Subdividing node #7 @ level 2.
Leaf node (59).
Subdividing node #6 @ level 2.
Leaf node (81).
Subdividing node #5 @ level 2.
Leaf node (77).
Subdividing node #3 @ level 1.
.. (212) 0 ms
Branch node.
Subdividing node #12 @ level 2.
Leaf node (46).
Subdividing node #11 @ level 2.
Leaf node (55).
Subdividing node #10 @ level 2.
Leaf node (55).
Subdividing node #9 @ level 2.
Leaf node (58).
Subdividing node #2 @ level 1.
.. (260) 15.626 ms
Branch node.
Subdividing node #16 @ level 2.
Leaf node (68).
Subdividing node #15 @ level 2.
Leaf node (69).
Subdividing node #14 @ level 2.
Leaf node (71).
Subdividing node #13 @ level 2.
Leaf node (53).
Subdividing node #1 @ level 1.
.. (240) 0 ms
Branch node.
Subdividing node #20 @ level 2.
Leaf node (68).
Subdividing node #19 @ level 2.
Leaf node (60).
Subdividing node #18 @ level 2.
Leaf node (62).
Subdividing node #17 @ level 2.
Leaf node (50).

Tree completed (21 nodes).

Load: 0 ms
Process: 109.377 ms

Done.

Когда попробовал с 10⁸ прямоугольники, BLOCK_SIZE из 64 тыс. записей для построения дерева с max_depth из 6. Это уже дает узлы с ок. 10⁵ элементы, которые могут быть легко обработаны с помощью алгоритма в памяти.

Программа использовала только несколько мегабайт ОЗУ для всего процесса.

Проверка на ошибки, модульные тесты (я не смог бы соответствовать коду здесь).
Добавьте метаданные в файл прямоугольника, чтобы вы могли найти, с какими полигонами они совпадают. Я бы сохранил размер записи кратным 16 байтам (выравнивание).
Распараллеливание
- Mutex для синхронизации quadtreeмьютекс для синхронизации stack, пул потоков для запуска for (; !work.empty();) { ... петля.
- Поскольку мы выдвигаем дочерние узлы только после того, как они были подразделены, каждый поток всегда будет работать в изолированном разделе дерева.
Гибридный подход
- Дисковый ввод / вывод становится узким местом в такой обработке. Как только мы доберемся до достаточно маленьких узлов (скажем, 10⁵ — 10⁶ записи), мы можем обрабатывать данные удобно в памяти.
- Используйте список узлов из этого алгоритма в качестве поиска, чтобы загрузить «маленькие» квадродеревы в памяти. Внедрите механизм кэширования, чтобы последние доступные «маленькие» квадродеревы оставались доступными.
Векторизация (возможно, может ускорить сопоставление большого количества прямоугольников).

6