gnuplot — спектрограмма с переполнением стека
Я пытаюсь сгенерировать спектрограмму синусоидального сигнала с C ++. Для генерации спектрограммы:
- Я разделил настоящий синусоидальный сигнал на блоки В
- Прикладное окно Хеннинга к каждому блоку (я предположил, что нет перекрытия). Это должно дать мне входные данные для БПФ.
- Приложил FFT к каждому блоку и рассчитал величину из частотных коэффициентов
u[i][0]а такжеu[i][1]и положить его вv[k][i]где k — количество блоков и выборок каждого окна - График времени
tt[k]противv[k][i]
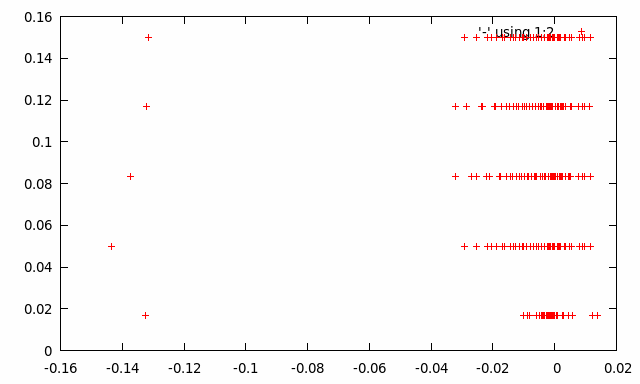
Это дает мне следующий сюжет:
Тем не менее, этот сюжет не выглядит правильным.
Какие-нибудь предложения, чтобы заставить это работать? Вот мой код:
#include <stdlib.h>
#include <stdio.h>
#include <time.h>
#include <fftw3.h>
#include <iostream>
#include <cmath>
#include <fstream>
using namespace std;
int main()
{
int i;
int N=500;//Number of points acquired inside the window
double Fs=200;//sampling frequency
int windowsize=100;//Number of samples in each block
double T=1/Fs;//sample time
double f=50;//frequency(Hz)
double *in;
fftw_complex *out;
double t[N];//time vector
double tt[5];
double v [5][249];
fftw_plan plan_forward;
in = (double*) fftw_malloc(sizeof(double) * N);
out = (fftw_complex*) fftw_malloc(sizeof(fftw_complex) * (N/2 + 1));
for (int i=0; i<= N;i++)
{
t[i]=i*T;
in[i] =0.7 *sin(2*M_PI*f*t[i]);// generate sine waveform
}
plan_forward = fftw_plan_dft_r2c_1d (windowsize, in, out, FFTW_ESTIMATE );
for (int k=0; k< 5;k++){
for (int i = 0; i<windowsize; i++){
double multiplier = 0.5 * (1 - cos(2*M_PI*i/(windowsize-1)));//Hanning Window
in[i] = multiplier * in[i+k*windowsize];
fftw_execute ( plan_forward );
v[k][i]=(20*log10(sqrt(out[i][0]*out[i][0]+ out[i][1]*out[i][1])))/N;//The magnitude in dB
}
}
for (int k=0; k< 5;k++){//Center time for each block
tt[k]=(2*k+1)*T*(windowsize/2);
}
fstream myfile;
myfile.open("example2.txt",fstream::out);
myfile << "plot '-' using 1:2" << std::endl;
for (int k=0; k< 5;k++){
myfile << v[k][i]<< " " << tt[k]<< std::endl;
}
myfile.close();
fftw_destroy_plan ( plan_forward );
fftw_free ( in );
fftw_free ( out );
return 0;
}
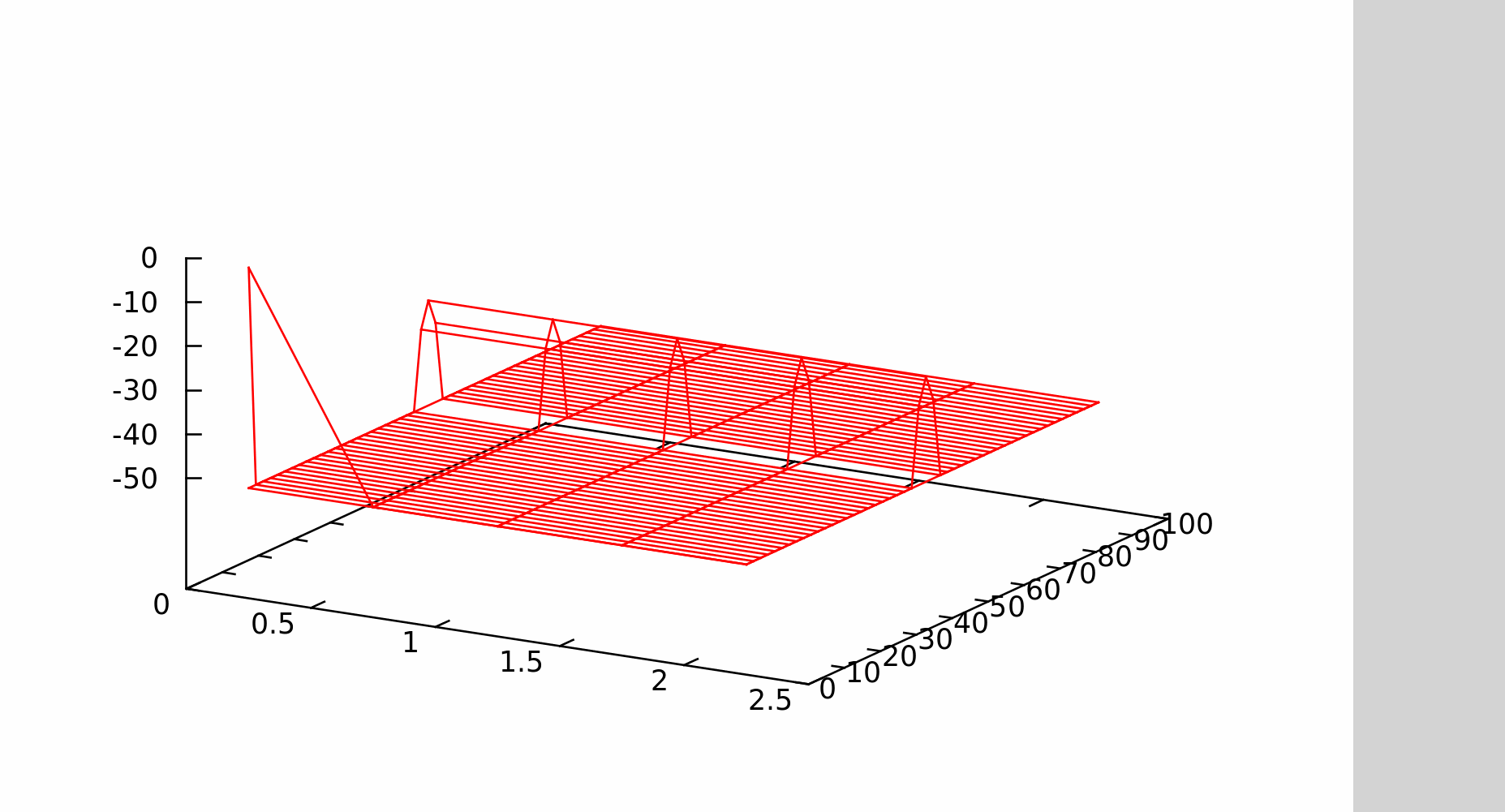
Решение
#include <stdlib.h>
#include <stdio.h>
#include <time.h>
#include <fftw3.h>
#include <iostream>
#include <cmath>
#include <fstream>
using namespace std;
int main()
{
int i;
int N=500;
double Fs=200;//sampling frequency
int windowsize=100;//Number of points acquired inside the window
double dF=Fs/N;
double T=1/Fs;//sample time
double f=50;//frequency
double *in;
fftw_complex *out;
double t[N];//time vector
double ff[N];
double tt[5];
double v [5][249];
fftw_plan plan_forward;
in = (double*) fftw_malloc(sizeof(double) * N);
out = (fftw_complex*) fftw_malloc(sizeof(fftw_complex) * (N/2 + 1));
for (int i=0; i<= N;i++)
{ t[i]=i*T;
in[i] =0.7 *sin(2*M_PI*f*t[i]);// generate sine waveform
}
plan_forward = fftw_plan_dft_r2c_1d (windowsize, in, out, FFTW_ESTIMATE );
for (int k=0; k< 5;k++){
for (int i = 0; i<windowsize; i++){
double multiplier = 0.5 * (1 - cos(2*M_PI*i/(windowsize-1)));//Hanning Window
in[i] = multiplier * in[i+k*windowsize];
}
fftw_execute(plan_forward);
for (int j = 0; j <= ((windowsize/2)-1); j++){
v[k][j] = 2*(out[j][0] * out[j][0] + out[j][1] * out[j][1])/(N*N);
v[k][0] *= 0.5;
v[k][N/2] *= 0.5;
for (int j = 0; j <= windowsize/2; j++){
v[k][j] = 10 * log10(v[k][j] + 1e-5);
}
}
for (int j = 0; j <= ((windowsize/2)-1); j++)
{ff[j]=Fs*j/windowsize;
}
//Center time for each block
for (int k=0; k< 5;k++){
tt[k]=(2*k+1)*T*(windowsize/2);
}
double b[6];
fstream myfile;
myfile.open("data.txt",fstream::out);
myfile << "plot '-' using 1:2" << std::endl;
for (int k=0; k< 6;k++) {
b[0]=5;
b[k+1]=tt[k];
myfile <<b[k] << "\t";
}
myfile<< std::endl;
for (int j = 0; j <= windowsize/2; j++){ myfile << ff[j]<< "\t";
for (int k=0; k< 5;k++){ myfile << v[k][j]<< "\t";
}
myfile<< std::endl;
}
myfile.close();
fftw_destroy_plan ( plan_forward );
fftw_free ( in );
fftw_free ( out );
return 0;
}
Другие решения