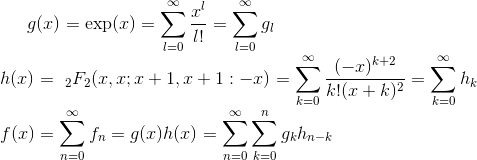GMP дает неверный результат расширения серии

Это учебник пример катастрофической отмены.

Слагаемые в серии 2F2 увеличиваются до максимального размера около exp (x), но величина функции 2F2 составляет около exp (-x). Это означает, что вам нужно использовать как минимум log_2 (exp (2x)) ~ = 2.886 * x дополнительные биты точности для точного вычисления ряда 2F2 и, возможно, немного больше в зависимости от того, как вычисляются члены.

Так, например, если x = 29, вам нужно около 83 бит точности. В вашем коде используется точность по умолчанию для типа MPF, которая, как мне кажется, составляет около 64 бит. Вам нужно изменить код, чтобы установить точность всех переменных MPF на 64 + 2,886 * x бит, чтобы получить 64 точных бита (см. Руководство по GMP, как это сделать).

На практике оценка ряда, которую вы реализовали, не очень эффективна и, вероятно, будет слишком медленной для x = 1e6.

Одна из возможностей заключается в использовании Арб библиотека (которую я разрабатываю). Это поддерживает вычисление обобщенных гипергеометрических функций из коробки и использует гораздо более эффективную стратегию оценки серии (в этом случае, используя двоичное расщепление). Он также использует интервальную арифметику, поэтому вы бесплатно получаете границы ошибок и можете установить точность автоматически, вместо того, чтобы заранее прогнозировать необходимую точность (но в этом случае прогнозировать точность легко и быстрее).

Вот код, демонстрирующий, как его использовать:

#include "acb_hypgeom.h"
int main()
{
acb_t z, t;
acb_struct a[2];
acb_struct b[2];
double x;

acb_init(z); acb_init(t);
acb_init(a + 0); acb_init(a + 1);
acb_init(b + 0); acb_init(b + 1);

for (x = 10.0; x <= 1000000; x *= 10)
{
acb_set_d(a + 0, x);
acb_set_d(a + 1, x);
acb_set_d(b + 0, x + 1);
acb_set_d(b + 1, x + 1);
acb_set_d(z, -x);
acb_hypgeom_pfq(t, a, 2, b, 2, z, 0, 64 + 2.886 * x);
acb_neg(z, z);
acb_exp(z, z, 64);
acb_mul(t, t, z, 64);
printf("f(%f) = ", x); acb_printn(t, 20, 0); printf("\n");
}

acb_clear(z); acb_clear(t);
acb_clear(a + 0); acb_clear(a + 1);
acb_clear(b + 0); acb_clear(b + 1);
}

Вот вывод:

f(10.000000) = [12.37067931727649929 +/- 5.38e-18]
f(100.000000) = [106.6161729468899444 +/- 4.93e-17]
f(1000.000000) = [1020.154983574938368 +/- 3.54e-16]
f(10000.000000) = [10063.00061277849954 +/- 2.57e-15]
f(100000.000000) = [100198.5001942224819 +/- 6.28e-14]
f(1000000.000000) = [1000626.990558714621 +/- 4.59e-13]

При x = 1e6 оценка занимает около 20 секунд (ваш код займет гораздо больше времени) в результате использования 2,9 миллиона битов. Если это все еще слишком медленно, вам нужно найти лучшую формулу для вычисления f (x), в идеале — асимптотическое расширение, допустимое, когда x -> бесконечность, или, возможно, интегральное представление (если оно существует без проблем отмены).

Теперь, если ваша функция 2F2 зависит только от x в последнем аргументе и имеет фиксированные первые четыре параметра, для этой асимптотики будет стандартная формула, но с учетом растущих параметров я не совсем уверен, как это сделать. , Так как верхний и нижний параметры почти «отменяют», это может сработать, чтобы рассматривать их как константы и использовать стандартные асимптотические ряды по аргументу, но я не проверял это. Кто-то с большим опытом в асимптотическом анализе должен был бы прокомментировать.

Также возможно, что вы могли бы использовать смежные отношения, чтобы уменьшить функцию 2F2 до чего-то с небольшими параметрами, но я не уверен, что это будет улучшение на практике.