глубокое обучение — Как сделать максимальный пул с Eigen :: Tensor Stack Overflow

Можем ли мы сделать максимальное объединение по трем измерениям с собственным тензором? Я пытался с методом сокращения без успеха.

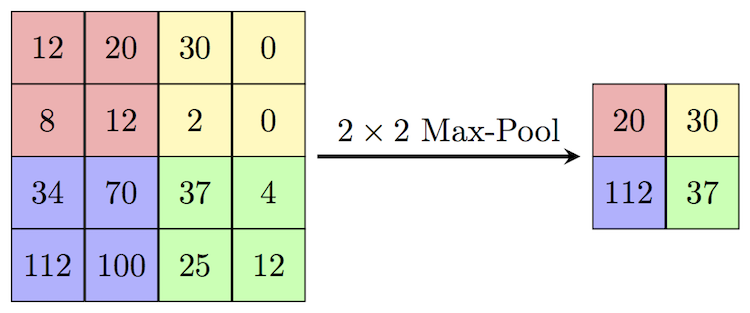
Я видел этот пример в собственном тесте.

struct UserReducer {
static const bool PacketAccess = false;
UserReducer(float offset) : offset_(offset) {}
void reduce(const float val, float* accum) { *accum += val * val; }
float initialize() const { return 0; }
float finalize(const float accum) const { return 1.0f / (accum + offset_); }

private:
const float offset_;
};

template <int DataLayout>
static void test_user_defined_reductions() {
Tensor<float, 2, DataLayout> tensor(5, 7);
tensor.setRandom();
array<ptrdiff_t, 1> reduction_axis;
reduction_axis[0] = 1;

UserReducer reducer(10.0f);
Tensor<float, 1, DataLayout> result = tensor.reduce(reduction_axis, reducer);
VERIFY_IS_EQUAL(result.dimension(0), 5);
for (int i = 0; i < 5; ++i) {
float expected = 10.0f;
for (int j = 0; j < 7; ++j) {
expected += tensor(i, j) * tensor(i, j);
}
expected = 1.0f / expected;
VERIFY_IS_APPROX(result(i), expected);
}
}

Я хочу уменьшить матрицу с максимальным фильтром 2×2 и получить шаг 2, но я не уверен, как это сделать, и если это правильный метод.

array<ptrdiff_t, 2> reduction_axis;
reduction_axis[0] = 0; reduction_axis[1] = 1;
MaxPool reducer;
Eigen::Tensor<float, 3, Eigen::ColMajor> max_pool(12, 12, 1);
max_pool = output.reduce(reduction_axis, reducer);