geometry — предпочтительное средство для нахождения общей касательной к паре эллипсов в переполнении стека
Я хочу сделать это на C ++. У меня есть две идеи, с помощью которых я могу сделать это:
- Рассматривая пару эллипсов как параметрические уравнения двух разных параметров, я могу получить два уравнения в терминах двух параметров. Эта пара уравнений нелинейная, обе функции котангенсов, синусов и косинусов. Geant4, с которым я в основном работаю, имеет только полином
- Используйте библиотеку геометрии, чтобы решить эту проблему. Я посмотрел на геометрию Boost, но документация бессвязна (для меня). Сказав это, он кажется более нацеленным на вычислительную геометрию. Возможно, я прошу это сделать Y, когда это было предназначено только для X.
Как можно пойти по этому поводу? В питоне это так просто, я мог бы сделать это во сне. Любое понимание будет высоко ценится. С тех пор, как я начал заниматься C ++, мне кажется, что выбор библиотеки для использования — это огромная битва сама по себе.
Решение
У меня есть несколько предложений. Вы можете попробовать LibreCAD, в котором есть решатель для общих касательных к двум эллипсам, но я ничего не знаю об API. Решатель решает уравнения четвертого порядка, что вы получаете, если наивно пытаетесь найти общие касательные для двух эллипсов.
Если вы хотите свернуть свое собственное: немного теории («диапазоны коник»), то, что вы просите, может быть сделано с помощью линейной алгебры (а именно, поиск инверсий матриц 3х3) плюс решение квадратичных и одного кубического уравнения. Это выглядит так:
Вы можете выразить любую конику (например, эллипс) в виде матричного уравнения
[m00 m01 m02] [x]
[x,y,z] [m10 m11 m12] [y] = 0
[m20 m21 m22] [z]
где матрица M симметричный и [x,y,z] являются однородными координатами; просто думай z=1, Мы можем записать это уравнение в краткой форме как X M X^T = 0 где X^T это транспонирование X,
Линии в плоскости можно записать в виде lx+my+nz=0 и так есть «координаты линии» (l,m,n),
Множество касательных к вышеуказанной конике может быть выражено очень просто в этих обозначениях. Позволять A быть обратной матрицей M, Множество касательных к коническому
[a00 a01 a02] (l)
(l,m,n) [a10 a11 a12] (m) = 0
[a20 a21 a22] (n)
Теперь предположим, что у нас есть вторая коника с матрицей Nи что N имеет обратное B, Общая касательная будет удовлетворять вышеуказанному уравнению и уравнению
[b00 b01 b02] (l)
(l,m,n) [b10 b11 b12] (m) = 0
[b20 b21 b22] (n)
Фактически мы можем скалярно умножить матрицу в последнем уравнении на t и он все равно будет держаться
[b00 b01 b02] (l)
(l,m,n) t [b10 b11 b12] (m) = 0
[b20 b21 b22] (n)
Добавляя уравнение для касательных к первой конике к приведенному выше уравнению для второй коники, получаем матричное уравнение L (A + tB) L^T = 0, Таким образом, любая общая касательная к двум коникам является общей касательной к каждой конике в «диапазоне» A + tB,
Теперь для большой упрощающей идеи: мы можем найти некоторые очень специальные коники в этом диапазоне, «вырожденные» коники, которые являются просто парами точек. Поскольку общие касательные должны проходить через все коники, из этого следует, что они должны проходить через вырожденные коники. Но легко найти линии, проходящие через вырожденные коники, поскольку такие коники — просто пары точек!
Вы можете найти вырожденные коники, решив кубическое уравнение det(A + tB) = 0 где det() определитель матриц 3х3. Кубика может быть решена в закрытой форме по формуле Кардано или вариации, или она может быть решена численно, если это то, что вам нужно. Как только вы найдете значение (я) t которые делают вырожденные коники, вы можете факторизовать уравнение L (A + tB) L^T = 0 на два линейных фактора. Каждый линейный фактор xl + ym + zn = 0 определяет точку в однородных координатах [x,y,z]или в декартовых координатах (x/z,y/z), Таким образом, вы должны получить три пары очков (шесть очков). Прохождение линий через определенные пары точек даст вам четыре (максимум) касательные линии.
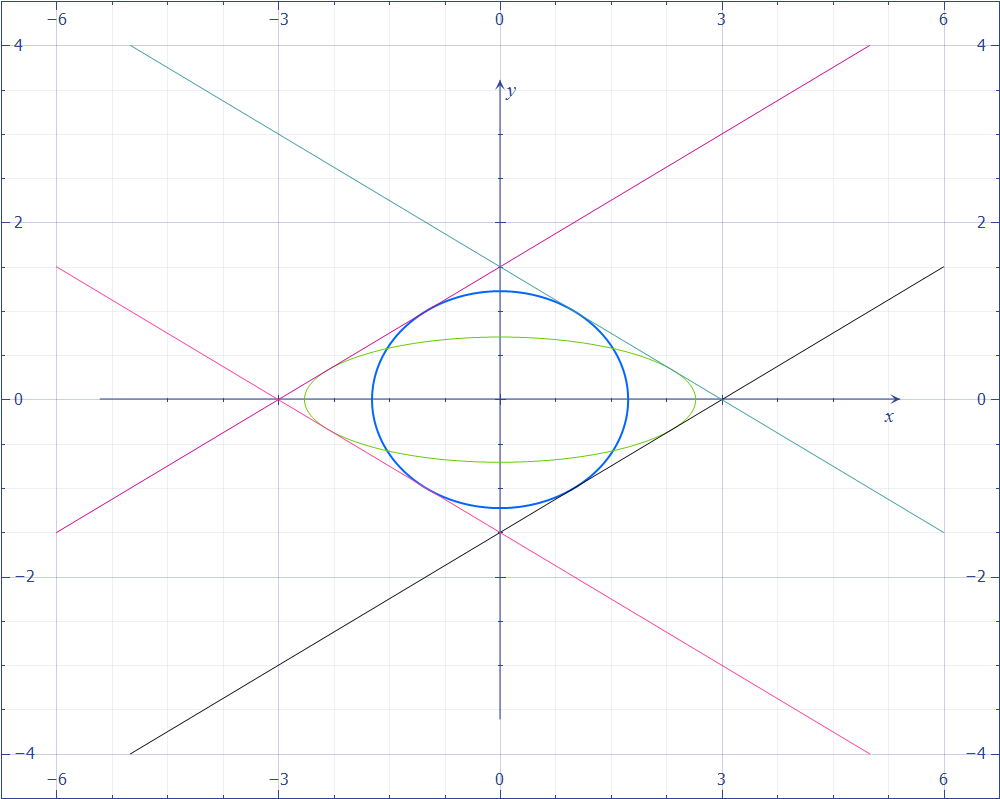
Вот простой пример (где центры двух эллипсов находятся в начале координат): найдите общие касательные к x^2+2y^2=3 а также x^2+14y^2=7, Конические в матричной форме являются
[1 0 0] [x] [1 0 0] [x]
[x,y,z] [0 2 0] [y] = 0, [x,y,z] [0 14 0] [y] = 0
[0 0 -3] [z] [0 0 -7] [z]
Касательные задаются
[6 0 0] (l) [14 0 0] (l)
(l,m,n) [0 3 0] (m) = 0, (l,m,n) [ 0 1 0] (m) = 0
[0 0 -2] (n) [ 0 0 -2] (n)
Обратите внимание, что я умножил обратные матрицы на скаляр только для того, чтобы сделать записи целыми, а не рациональными числами. Вам не нужно этого делать, но это облегчает ручные вычисления. Умножение второй матрицы на дополнительный скаляр t дает
[6+14t 0 0 ] (l)
(l,m,n) [0 3+t 0 ] (m) = 0
[0 0 -2-2t] (n)
Коника вырождена, когда (6+14t)(3+t)(-2-2t)=0то есть когда t=-3/7, -3, -1, когда t=-3/7 мы получаем
18/7 m^2 - 8/7 n^2 = 2/7 (9 m^2 - 4 n^2) = 2/7 (3m - 2n)(3m + 2n) = 0
Это соответствует точкам с однородными координатами [x,y,z] = [0,3,-2] а также [0,3,2]другими словами, к точкам с декартовыми координатами (0,-3/2) а также (0,3/2),
когда t=-3 мы получаем -36l^2 + 4n^2 = (6l+2n)(-6l+2n) = 0, точки [6,0,2] а также [-6,0,2] или в декартовых координатах (3,0) а также (-3,0), Наконец, когда t=1 мы получаем -8l^2 + 2m^2 = 2(2l+m)(-2l+m) = 0 в соответствии с точками [2,1,0] а также [-2,1,0] которые являются точками в бесконечности.
Пока мы избегаем точек на бесконечности, просто потому, что с ними немного сложнее работать, мы получаем четыре строки через следующие пары точек:
{(0,-3/2),(-3,0)}, {(0,-3/2),(3,0)}, {(0,3/2),(-3,0)}, {(0,3/2),(3,0)}
которые дают нам четыре общих касательных к двум эллипсам.
Из рисунка видно, что общие касательные также проходят через точки на бесконечности [2,1,0] а также [-2,1,0]то есть, что пары параллельных линий имеют наклон 1/2 а также -1/2,
Разве это не красиво?
Другие решения