геометрия — пересечение лучей и треугольников в переполнении стека
Мне дали пример кода, который мне нужно исправить, и одна функция, которую мне нужно создать, будет использоваться для трассировки лучей треугольника. В настоящее время я настроил код, подобный этому.
/*RayHitResult is a struct that determines if the ray has reached a polygon*/
RayHitResult TriangleIntersect(Ray& ray)
{
RayHitResult result = Ray::s_defaultHitResult;
double t = 10000; /*This is an extreme value for testing*/
Vector3 point;
Vector3 edge1 = m_vertices[1] - m_vertices[0]; /*m_vertices[0], [1] and [2] are the vertices of the triangle*/
Vector3 edge2 = m_vertices[2] - m_vertices[0];
Vector3 t_normal = edge1.CrossProduct(edge2); /*This is the normal*/
double d = -(m_vertices[0].DotProduct(t_normal)); /*This is the offset*/
t = -(ray.GetRayStart().DotProduct(t_normal) + d) / (ray.GetRay().DotProduct(t_normal)); /*The variable t is what I need to calculate*/
point = ray.GetRayStart() + ray.GetRay()*t;
/*This statement alters the result depending on whether there was an intersection*/
if (t > 0 && t < 10000)
{
result.t = t;
result.normal = this->m_normal;
result.point = point;
result.data = this;
return result;
}
return result;
}
Мне нужно вычислить значение переменной «t», чтобы определить, пересек ли луч с многоугольником. Однако текущее уравнение, используемое для вычисления «t», является неверным, поскольку оно не дает определенного результата. Мне сказали, что формула, которую я использую, является правильной, поэтому кто-нибудь может сказать мне, почему текущее уравнение «t» не работает?
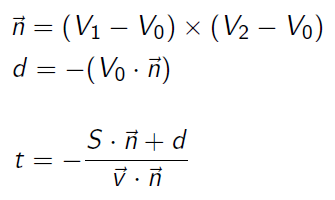
n — нормаль, d — смещение, S — начало луча, а v — сам луч.
Решение
Мне всегда проще всего вывести эти уравнения с нуля.
Треугольник можно рассматривать как начало координат o и 2 векторов u и v.
o + au + bv указывает плоскость.
Итак, сначала вы берете свой луч k + tl и находите значение t, где этот луч пересекается с этой плоскостью.
Похоже, это то, что делает ваш кусок кода.
(Обратите внимание, что существует очень малая вероятность того, что луч летит параллельно плоскости, и столкновения не произойдет; вы захотите проверить, правильно ли ваш код обрабатывает потенциал, деленный на 0)
Давайте назовем эту точку столкновения с.
Но работа еще не сделана. Задача теперь состоит в том, чтобы определить, находится ли s внутри треугольника.
Если вы можете выразить s как o + au + bv, то проверка a и b даст вам ответы.
И если a и b ОБА между 0 и 1, то точка находится внутри параллелограмма с началом o и ребрами a и b.
Кроме того, если a + b < 1 точка находится в пределах его нижнего ТРЕУГОЛЬНИКА.
Другие решения
