Геометрическое искажение, показывающее черное изображение

Question

Геометрическое искажение, показывающее черное изображение

У меня возникла проблема с геометрическим искажением, в основном искажением изображения в перспективе сверху вниз. Без использования очков.

Что я имею:

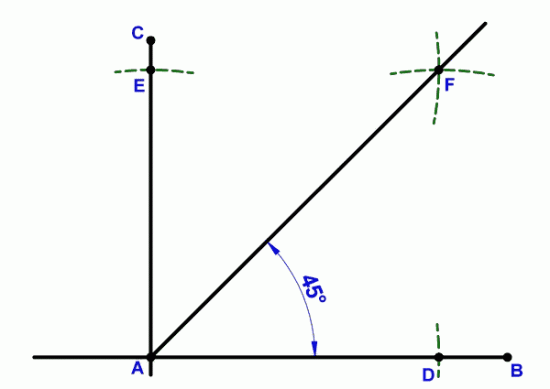
У меня есть изображение, смотрящее под углом 45 градусов (т.е.) F — это местоположение моей камеры, направленное вниз
это бумага о том, что я хочу сделать. Страница 2 имеет основную формулу
Основная функция, используемая в opencv cv::warpPerspective активировать это искаженное изображение
У меня есть необходимое вращение Ccam1_cam2 (при условии, что моя математика верна)

Что я сделал:

Я сгенерировал матрицу H, используя формулу из статьи.
Проверено, не было ли перевода только вращение, т.е. H=R если это сделает искаженное изображение лучше.

Посмотрел на мои значения x, y из искаженного изображения и заметил, что они <1, что плохо, потому что они должны быть в диапазоне 400×530, который является исходным изображением.

Код:

cv::Mat  hmatrix = (cv::Mat_<double>(3,3) << H.c11, H.c12, H.c13,
H.c21, H.c22, H.c23,
H.c31, H.c32, H.c33);
lfImg = cv::imread("undistortedsmall.bmp", 0);
imshow("not warped image", lfImg);
cv::waitKey(0);
cv::Mat warpedimg;
cv::Scalar borderValue;
cv::warpPerspective(lfImg, warpedimg, hmatrix ,lfImg.size(),cv::INTER_LINEAR,cv::BORDER_CONSTANT,borderValue);

imshow("warpedImage", warpedimg);

Я взял точки с изображения сверху вниз с соответствующими точками из моего изображения 45 градусов и сгенерировал H-матрицу, которая хорошо деформируется. Просто чтобы посмотреть, как может выглядеть H-матрица. Но масштаб совсем другой.

пример:

 My generated H Matrix:
0.240053 0.859119 -0.451983
0.689905 -0.478534 -0.543171
-0.682938 -0.181435 -0.707585

pt generated H matrix
0.894764 3.37653 77.6052
-0.950235 2.02846 240.977
-8.73899e-05 0.00384326 1

Что я хочу:

Нисходящая деформация этого изображения без использования точек, извлеченных из изображения.

Эта проблема
Черный экран (если я масштабирую матрицу, скажем, несколько кратных * 100)
Я получаю неправильную деформацию, но, по крайней мере, что-то видимое

1

c++homography opencv perspective transformation

Решение

Другие решения

Источник

Accepted Answer

Так как вы не показали полный код, который генерирует значения в H — трудно сказать наверняка, но вы можете пропустить матрицу внутренних параметров (также часто называемую матрицей калибровки камеры).

Это не упоминается в предоставленной вами статье, что означает, что они работают с так называемой «нормализованной» или «некалиброванной» гомографией. Когда вы генерируете гомографию из точечных соответствий, вы получаете «калиброванную» гомографию и получаете ожидаемые результаты.

Рассмотреть раздел Уравнение трехмерной плоскости Вот. Как вы можете видеть, R- (t * n ^ t) / d предварительно умножается на матрицу Ka и затем умножается на Kb ^ -1 (внутренняя матрица инвертированной второй камеры), чтобы получить «калиброванную» гомографию. Если оба изображения сделаны одной и той же камерой, вы можете принять Ka = Kb.

Таким образом, для получения «калиброванной» гомографии вы можете использовать выражение Hc = K * H * K ^ -1, где Hc — калиброванная гомография, H — некалиброванная гомография, а K — калибровочная матрица.

Теперь вам нужно рассчитать K. В идеале вам нужно выполнить калибровку камеры, чтобы получить ее, но если вы знаете фокусное расстояние камеры, вы можете использовать несколько грубое приближение следующим образом:

    | f, 0, cx |
K = | 0, f, cy |
| 0, 0,  1 |

где f — фокусное расстояние камеры в пикселях, а (cx, cy) — координаты главной точки (вы можете использовать (w / 2, h / 2), где w и h — ширина и высота изображения в пикселях)

0