генерация синусоидальной волны в переполнении стека

Question

генерация синусоидальной волны в переполнении стека

Я пытаюсь сгенерировать набор точек, которые при построении графика представляют синусоидальную волну 1 цикла. Требования следующие:

синусоида 1 цикла
нижний предел = 29491
верхний предел = 36043
Нет баллов = 100
Амплитуда = 3276
смещение нуля = 32767

Код:

int main()
{
ofstream outfile;
outfile.open("data.dat",ios::trunc | ios::out);
for(int i=0;i<100;i++)
{
outfile << int(3276*sin(i)+32767) << "\n";
}
outfile.close();
return 0;
}

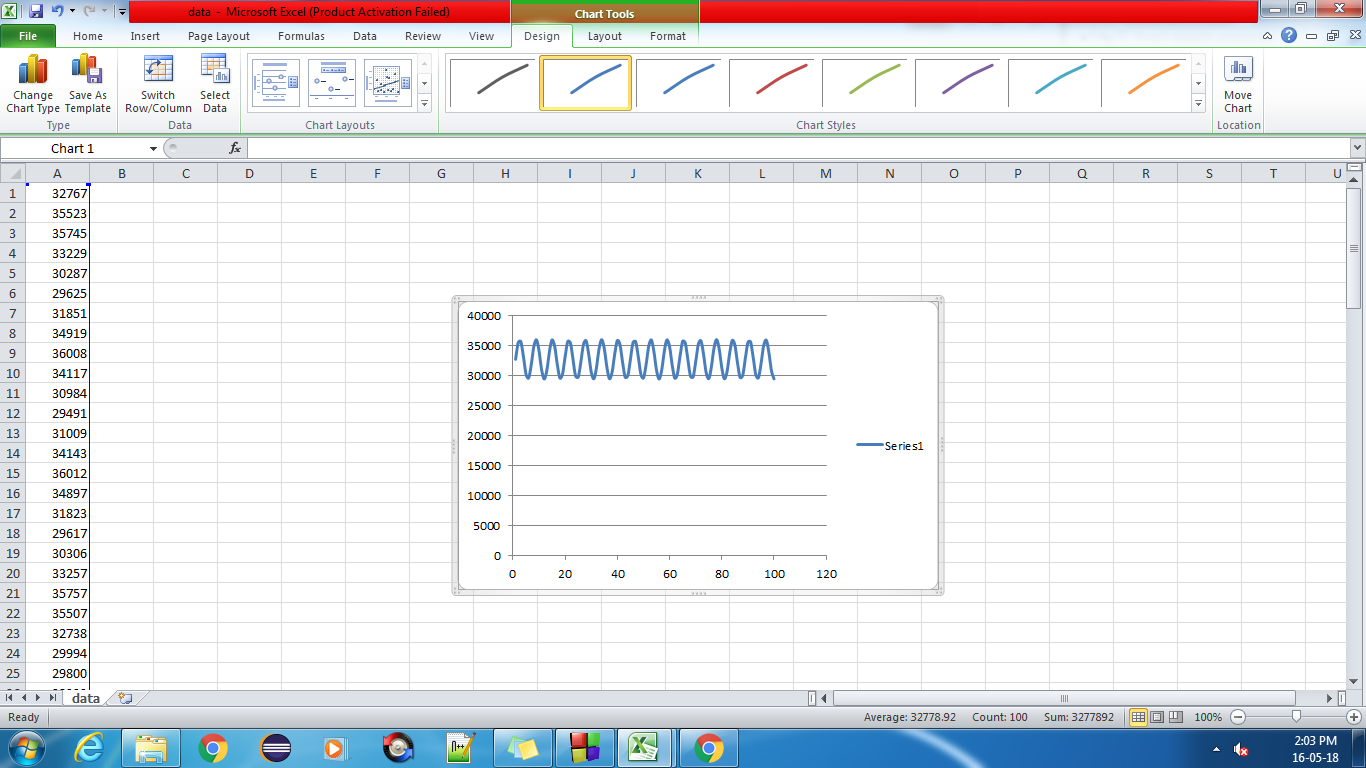
Я генерирую и храню точки в файле. Когда эти точки нанесены, я получаю следующий график.

Но мне нужен только один цикл. Как я могу это сделать?

0

c++sin sine

Решение

Другие решения

принимая в формулу синусоидальная волна:

y(t) = A * sin(2 * PI * f * t + shift)
где:

А = амплитуда, пик отклонения функции от нуля.
f = обычная частота, количество колебаний (циклов)
t = время
сдвиг = сдвиг фазы

было бы:

y[t] = AMPLITUDE * sin (2 * M_PI * 0.15 * t + 0) + ZERO_OFFSET;
^^^ f = 15 cycles / NUM_POINTS = 0.15 Hz

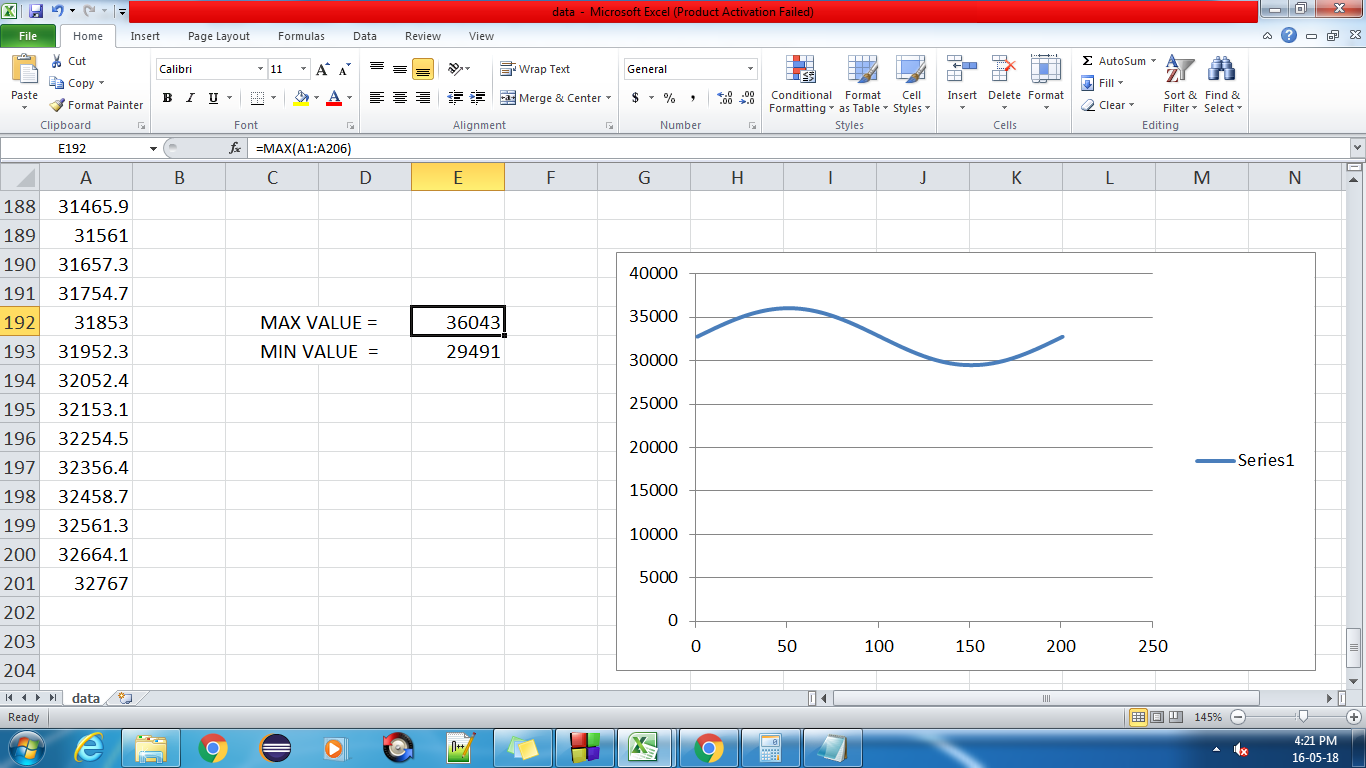
Чтобы иметь один полный цикл, цикл из y[0:t) где t это время или количество точек, необходимых для полного цикла (то есть длины волны)

2

Вам нужно изменить цикл for для итерации от 0 до 2 (пи). Это один цикл для синусоиды. Вы также можете изменить счетчик цикла на двойное вместо целого и увеличить на 0,1 или что-то в этом роде.
скриншот от WolframAlpha.com

0

Математическая функция синуса станд :: грех принимает аргумент в радианах:

arg — значение, представляющее угол в радианах, с плавающей точкой или
Интегральный тип

Если вам нужен 1 цикл и 100 баллов, то, зная, что в одном цикле есть радианы 2pi, вам нужно что-то вроде

double rads;
for(int i=1;i<=100;i++)
{
rads = 2.0*M_PI*i/100;
// your expression in terms of std::sin(rads)
}

Если по случайности ваш компилятор / библиотека не имеет M_PI из коробки, тогда посмотрите Вот для флагов, которые должны сделать его доступным.

Одна вещь, которая не была затронута — это точный интервал, который вы должны сгенерировать. Если вам нужен закрытый интервал [0,2pi], вам нужно будет отрегулировать размер шага. Я дал полуоткрытый интервал (0,2pi), а @Michael Walz дал другой полуоткрытый интервал [0,2pi).

0

Полный цикл состоит из 360 градусов. необходимых образцов составляет 100.
Таким образом, размер шага составляет 3,6. Я пропустил это раньше.

int main()
{
ofstream outfile;
outfile.open("data.dat",ios::trunc | ios::out);
for(int i=0;i<101;i++)
{
float rads = M_PI/180;
outfile << (float)(3276*sin(3.6*i*rads)+32767) << endl;
}
outfile.close();
return 0;
}

Если количество образцов составляет 200, то размер шага, если 360/200 = 1.8

int main()
{
ofstream outfile;
outfile.open("data.dat",ios::trunc | ios::out);
for(int i=0;i<201;i++)
{
float rads = M_PI/180;
outfile << (float)(3276*sin(1.8*i*rads)+32767) << endl;
}
outfile.close();
return 0;
}

Выход:

0

Источник

Accepted Answer

Похоже, вам нужно 100 выборок за один цикл, поэтому вам, вероятно, нужно это:

...
#define _USE_MATH_DEFINES
#include <math.h>
...
#define NB_OF_SAMPLES 100
...
double angle = 0.0;
for (int i = 0; i < NB_OF_SAMPLES; i++)
{
outfile << int(3276 * sin(angle) + 32767) << "\n";
angle += (2 * M_PI) / NB_OF_SAMPLES;
}
...

Или лучше:

#define NB_OF_SAMPLES 100
#define OFFSET        3276
#define AMPLITUDE     32767

...
double angle = 0.0;
for (int i = 0; i < NB_OF_SAMPLES; i++)
{
outfile << int(AMPLITUDE * sin(angle) + OFFSET) << "\n";
angle += (2 * M_PI) / NB_OF_SAMPLES;
}
...

2