Генерация нормальных распределительных весовых констант в диапазоне
У меня есть некоторые результаты, актуальность которых уменьшается с расстоянием. Я хочу взвешивать элементы результирующего массива с константами, распределение которых близко к нормальному или сложенному нормальному. При запуске я хочу сгенерировать массив с N константами, начиная с 1 до 0,01, функцией.
Результатом должно быть что-то вроде следующего, заканчивающееся числом, близким к 0,01.
const double normalDistWeight[] = {
1.000, 0.997, 0.994, 0.989, 0.984, 0.977, 0.970, 0.961, 0.951, 0.939,
0.926, 0.910, 0.893, 0.874, 0.853, 0.830, 0.805, 0.778, 0.750, 0.719,
0.687, 0.654, 0.619, 0.584, 0.548, 0.512, 0.476, 0.440, 0.405, 0.370,
0.337, 0.305, 0.274, 0.246, 0.219, 0.194, 0.171, 0.150, 0.131, 0.114,
0.098, 0.085, 0.073, 0.063, 0.054, 0.047, 0.040, 0.035, 0.030, 0.027
};
К сожалению, я не могу использовать какие-либо сторонние библиотеки или функции C ++ 11, только обычный C ++.
Редактировать: О, я слишком обдумывал это … Это просто простая ошибка Гаусса, поэтому exp (-x ^ 2) должна работать.
Решение
Мне кажется, что все, что вы хотите, это массив значений Гауссова функция соответствует равномерно расположенным точкам на положительной полуоси, вплоть до точки, где значение составляет около 0,01.
Это просто. Гауссова функция е(Икс) = Ехр (-Икс2), как это:
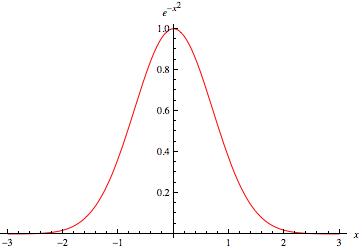
В выбранном выражении мы уже имеем е(0) = 1, так что остается только найти конечную точку Икс где у нас есть е(Икс) = 0,01. Инверсия: Икс = √ − log (0,01) ≈ 2,15.
Так что все, что вам нужно сделать, это оценить е на равномерно расположенных точках на отрезке [0, 2.15].
Другие решения
