Где я могу хранить фигуры в октри?
Пока немного информации о проектных решениях … Я разработал структуру октодеревьев, которая может хранить точки. Я решил ограничить рекурсию «поколений» на основе определенного базового размера вокселя. Дочерние узлы создаются только при добавлении точек к этому узлу. Это не динамическое графическое приложение — это дерево октавы и объекты в нем статичны, поэтому предварительная обработка для повышения производительности не является проблемой.
Теперь я хотел бы добавить «формы» к моей октри — в частности, поверхностную сетку, состоящую из треугольников. Вершины этих треугольников не соответствуют точкам, хранящимся в октое. Как хранить эти формы в октри? Я вижу два варианта …
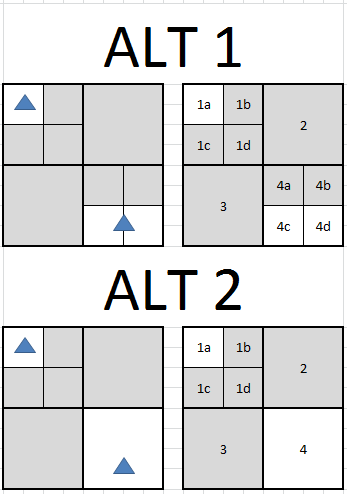
Серые узлы «пусты» в том смысле, что у них нет фигур. В альтернативе 1 фигуры сохраняются в каждом узле, который они пересекают, то есть узел 1a содержит shape1 и 4c. & 4d поделиться shape2. В альтернативе 2 фигуры хранятся только в наименьшем узле, который они пересекают — то есть узел 1a содержит shape1, а узел 4 содержит shape2.
Большинство постов на октреях, которые я видел, предполагают Alt1, но они никогда не объясняют почему. Alt2 имеет больше смысла для меня и будет создавать дополнительную работу только для тех фигур, которые находятся на границах узлов. Почему Alt1 предпочтительнее?
Изменить: чтобы уточнить, мой язык реализации используется C ++, поэтому я бы предпочел примеры реализации на этом языке, но вопрос не зависит от языка. Извините, если это неверное использование тега.
Edit2: хотя и не имеет прямого отношения к вопросу хранения формы, эта ссылка имеет хорошее обсуждение обхода октри, что стоит за вопросом. Я подумал, что это может помочь всем, кто заинтересован в работе над этим вопросом.
Обновить: Четыре года спустя Alt2 оказался проще в реализации, но очень медленным, потому что большие треугольники, хранящиеся на более высоких уровнях октри, тестировались при каждом обходе октре — в моем случае это означало от сотен до тысяч ненужных тестов. Я закончил пересмотр моего кода, чтобы использовать R * -деревянный вариант вместо этого, что было легко реализовать и существенно быстрее.
Решение
ALT1 правильный. Учитывая, что вы хотите ограничить максимальное количество объектов (треугольников) в узле, вам нужно будет подразделить узлы, которые будут содержать много треугольников. Это неизбежно приводит к наличию одного треугольника в нескольких узлах, если только вы не хотите разделить треугольники так, чтобы они идеально подходили к узлам октодерева (это зависит от вашего приложения, я, как правило, не рекомендовал бы это и, например, для трассировки лучей это обычно обычно не делается) ,
Как контрпример, представьте ALT2, содержащий детальную модель кролика Стэнфорда, стоящего на большом треугольнике. Большой треугольник предотвратит подразделение корневого узла на подузлы, и, следовательно, ваше октре будет так же хорошо, как если бы у вас не было октерева.
С другой стороны, вам придется сохранить большой треугольник в корневом узле и подразделить его на подузлы, которые будут содержать остальные меньшие треугольники кролика. Наличие треугольников не только в листовых узлах, но и в других узлах, вероятно, усложнит обход октре (но это также зависит от вашего приложения). Если мы придерживаемся сценария трассировки лучей, чтобы найти ближайшее пересечение луча и треугольника, вам придется проверить узел а также все подузлы, чтобы найти ближайшее пересечение, и вам нужно будет отслеживать движение луча к следующему узлу, на все уровни дерева одновременно. С другой стороны, если ваша геометрия находится только на листьях, вы проверяете треугольники на листьях в том порядке, в котором их посещает луч (отслеживая треугольники, которые уже были проверены, чтобы избежать проверки одного и того же треугольника дважды).
Другие решения
Это больше относится к quadtrees с которым я более знаком, но они являются 2D-эквивалентом октодерева; так что это может быть применимо.
Общие подходы к вставке: каждый внутренний узел дерева квадрантов имеет емкость, которая является максимальным количеством «объектов», которые может содержать квадрант дерева квадрантов. Если вы достигли емкости, вы подразделяете и затем вставляете все «объекты» в соответствующий дочерний квадрант. У вас также будет точка, в которой вы будете подразделять, и один или несколько ваших «объектов» пересекают несколько дочерних квадрантов; будьте осторожны в этом случае при вставке / запросе. Как правило, емкость узла выбирается либо для ускорения вставки, либо для запроса.
Итак, принимая это во внимание, я не вижу ничего плохого в изображении ALT2, которое вы представляете. Но мое предположение о том, почему вы всегда видите изображение ALT1, является подходом по умолчанию при вставке в незанятую ячейку — это подразделение, а затем вставка.
