Формула для ПИ-регулирования Пропорционально-интегральный алгоритм
Я читал этот сайт: http://www.csimn.com/CSI_pages/PIDforDummies.html и я запутался насчет пропорциональной составной части. Вот что это говорит.
Пропорциональный контроль
Вот схема контроллера, когда мы включили только управление P:
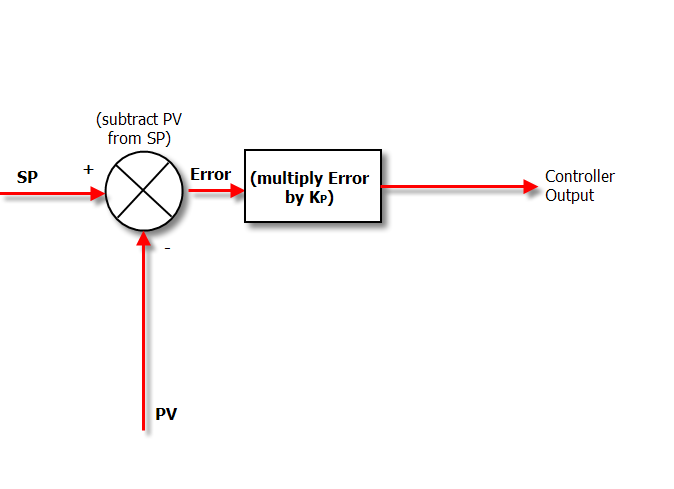
В режиме «Пропорционально» контроллер просто умножает ошибку на Пропорциональное усиление (Kp), чтобы получить выход контроллера.
Пропорциональное усиление — это настройка, которую мы настраиваем, чтобы получить желаемую производительность от контроллера «P only».
Матч, заключенный на небесах: P + I Controller
Если мы объединим пропорциональное и интегральное действие, мы получим скромный PI-контроллер. Диаграмма ниже показывает, как рассчитывается алгоритм в ПИ-контроллере.
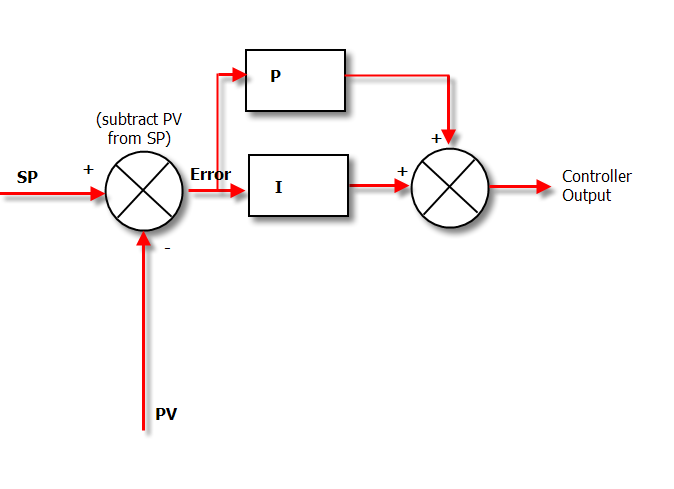
Сложность в Integral Action заключается в том, что он действительно испортит ваш процесс, если вы точно не знаете, сколько Integral action нужно применить.
Хорошая техника настройки PID точно подсчитает, сколько Integral нужно подать для вашего конкретного процесса, но как в первую очередь настраивается Integral Action?
Как видите, пропорциональная часть легко понять, это говорит о том, что вы умножаете ошибку на настройку переменной. Часть, которую я не получаю, это то, откуда вы берете P и I во второй части, и какую математическую операцию вы делаете с ними. У меня нет диплома по математике или углубленных знаний по исчислению, поэтому я был бы признателен, если бы вы попытались сохранить его на уровне алгебры.
Решение
Интегральная часть — это просто суммирование, умноженное на некоторую константу
- Аналоговое интегрирование осуществляется с помощью нелинейного усиления и усилителя.
-
Цифровая интеграция первого порядка — это просто:
output += input*dt; -
Второй порядок:
temp += input*dt; output += temp*dt; -
dt — продолжительность цикла итерации (таймер или что-либо еще)
-
не забывайте, что регулятор PI может иметь более сложный ответ
i1 += input*dt; i2 += i1*dt; i3 += i2*dt; output = a0*input + a1*i1 + a2*i2 +a3*i3 ...; -
где а0 — часть P
Теперь регулятор I добавляет все больше и больше значения контроля
- пока контролируемое значение не станет таким же, как заданное значение
- чем дольше требуется, чтобы соответствовать ему, тем быстрее он контролирует
- это создает быстрые колебания вокруг заданного значения
- по сравнению с P с тем же усилением
- но в среднем время управления меньше, чем у просто P регуляторов
- поэтому усиление I обычно намного меньше, что создает эффект памяти и сглаживания, упомянутый LutzL. (хотя время регулирования аналогично или меньше, чем просто для регулирования P)
Контролируемое устройство имеет свой собственный ответ
- это можно представить как дифференциальную функцию
- в кибернетике много теории о получении правильного ответа регулятора
- чтобы соответствовать вашим потребностям процесса как:
- качество контроля
- время реакции
- максимальная амплитуда колебаний
- стабильность
- но для всего вам нужна дифференциальная математика, как решение система дифференциальных уравнений любого порядка
- настоятельно рекомендуем использовать Преобразование Лапласа
- но многие люди также используют Z преобразование вместо
Таким образом, I-регулятор добавляет скорость к регулированию
- но это также создает большие колебания
- и когда не соответствует регулируемая система должным образом также создает нестабильность
- Интеграция добавляет риски переполнения в регулирование (аналоговая интеграция очень чувствительна к этому)
Также имейте в виду, что вы также можете вычесть часть I из контрольного значения.
- который сделает прямо противоположное
- иногда комбинация большего количества частей I используется для соответствия желаемой форме реакции регулирования
Другие решения
В тексте пропущена большая часть: физическая система, которая превращает управление в процесс, и физическая переменная.
Думайте об интеграле как о некой операции усреднения, которая отфильтровывает небольшие колебания на входе PV. Это также представляет собой некое воспоминание о недавнем прошлом процесса.
Например, можно представить, что скользящее экспоненциальное среднее представляет собой смесь интегрального и пропорционального действия.
Следуя примеру с вождением автомобиля, если вы придете к бордюру, где вам нужно, чтобы рулевое колесо находилось в определенном положении, чтобы двигаться по кругу, вы не просто дергаете колесо в это положение, вы перемещаете его постепенно (большую часть времени ). Именно такие действия по увеличению и уменьшению являются следствием использования составной части действия.
