FFT Spectrum не отображается правильно

В настоящее время я пытаюсь отобразить аудио спектр, используя FFTW3 и SFML. Я следовал найденным указаниям Вот и просмотрел многочисленные ссылки на БПФ, спектры и БПФ, но почему-то мои столбики почти все выровнены по левому краю, как показано ниже. Еще одна проблема, с которой я столкнулся, это то, что я не могу найти информацию о масштабах вывода FFT. В настоящее время я делю это на 64, но иногда оно выходит за рамки этого. Более того, я не нашел никакой информации о том, почему выходные данные из FFTW должны быть того же размера, что и входные данные. Итак, мои вопросы:

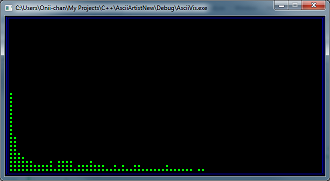
1. Почему большая часть моего спектра выровнена по левому краю, в отличие от изображения ниже моего?
2. Почему не выводится между 0,0 и 1,0?
3. Почему счетчик входных выборок связан с счетчиком выходных БПФ?

Что я получаю:

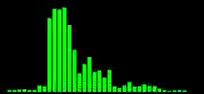
Что я ищу:

const int bufferSize = 256 * 8;

void init() {
sampleCount = (int)buffer.getSampleCount();
channelCount = (int)buffer.getChannelCount();
for (int i = 0; i < bufferSize; i++) {
window.push_back(0.54f - 0.46f * cos(2.0f * GMath::PI * (float)i / (float)bufferSize));
}
plan = fftwf_plan_dft_1d(bufferSize, signal, results, FFTW_FORWARD, FFTW_ESTIMATE);
}
void update() {
int mark = (int)(sound.getPlayingOffset().asSeconds() * sampleRate);
for (int i = 0; i < bufferSize; i++) {
float s = 0.0f;

if (i + mark < sampleCount) {
s = (float)buffer.getSamples()[(i + mark) * channelCount] / (float)SHRT_MAX * window[i];
}

signal[i][0] = s;
signal[i][1] = 0.0f;
}
}
void draw() {
int inc = bufferSize / 2 / size.x;
int y = size.y - 1;
int max = size.y;
for (int i = 0; i < size.x; i ++) {
float total = 0.0f;
for (int j = 0; j < inc; j++) {
int index = i * inc + j;
total += std::sqrt(results[index][0] * results[index][0] + results[index][1] * results[index][1]);
}
total /= (float)(inc * 64);
Rectangle2I rect = Rectangle2I(i, y, 1, -(int)(total * max)).absRect();
g->setPixel(rect, Pixel(254, toColor(BLACK, GREEN)));
}
}