что за алгоритм генерации карты высот из контурной линии?
Я ищу интерполяцию некоторых контурных линий для создания трехмерного изображения. Контуры не сохраняются на рисунке, координаты каждой точки контура просто сохраняются в std :: vector.
для выпуклых контуров:


, кажется (я сам не проверял), что высоту можно легко рассчитать (линейная интерполяция), используя расстояние между двумя ближайшими точками двух ближайших контуров.
мои контуры не обязательно выпуклые:


, так что это сложнее … на самом деле я понятия не имею, какой алгоритм я могу использовать.
Я закончил писать пример дискретного Лапласа:
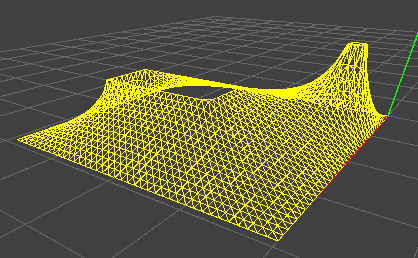
Вы можете получить код Вот
Решение
То, что у вас есть, в основном классический Проблема Дирихле:
Учитывая значения функции на границе области пространства, присвойте значения функции внутри области так, чтобы она удовлетворяла определенному уравнению (например, Уравнение Лапласа, что по существу требует, чтобы функция не имела произвольных «неровностей») везде внутри.
Существует много способов вычисления приближенных решений задачи Дирихле. Простой подход, который должен хорошо подходить к вашей проблеме, состоит в том, чтобы начать с дискретизации системы; то есть вы берете конечную сетку значений высоты, назначаете фиксированные значения тем точкам, которые лежат на контурной линии, а затем решаете дискретную версию уравнения Лапласа для оставшихся точек.
Теперь, что уравнение Лапласа на самом деле определяет, в простых терминах, это то, что каждая точка должна иметь значение, равное среднему ее соседей. В математической формулировке уравнения мы требуем, чтобы это сохранялось в пределе, поскольку радиус окрестности стремится к нулю, но поскольку мы фактически работаем над конечной решеткой, нам просто нужно выбрать подходящую фиксированную окрестность. Несколько разумных вариантов окрестностей включают в себя:
- четыре ортогонально смежные точки, окружающие центральную точку (например, окрестности фон Неймана),
- восемь ортогонально и диагонально смежных точек сетки (a.k.a. Окрестности Мура), или же
- восемь ортогонально и диагонально смежных точек сетки, взвешенных таким образом, чтобы ортогонально смежные точки учитывались дважды (по существу, сумма или среднее из двух вышеупомянутых вариантов).
(Из приведенных выше вариантов последний обычно дает наилучшие результаты, так как он наиболее близко соответствует Гауссово ядро, но первые два часто почти так же хороши, и могут быть быстрее, чтобы рассчитать.)
После того как вы выбрали окрестность и определили фиксированные граничные точки, пришло время вычислить решение. Для этого у вас есть два варианта:
-
Определить система линейных уравнений, по одному на каждую (неограниченную) точку сетки, утверждая, что значение в каждой точке является средним значением ее соседей, и реши это. Как правило, это наиболее эффективный подход, если у вас есть доступ к решатель разреженной линейной системы, но написание одного с нуля может быть сложной задачей.
-
Используйте итеративный метод, в котором вы сначала назначаете произвольное начальное предположение для каждой точки сетки без ограничений (например, используя линейную интерполяцию, как вы предлагаете), а затем зацикливаетесь на сетке, заменяя значение в каждой точке на среднее значение ее соседей. Затем продолжайте повторять это, пока значения не перестанут меняться (сильно).
Другие решения
Вы можете создать Ограниченная триангуляция Делоне из вершин и отрезков, описывающих контуры, затем используйте высоту, определенную в каждой вершине, в качестве координаты Z.
Получившаяся триангуляция может быть визуализирована как любой другой суп из треугольников.
Несмотря на название, вы можете использовать TetGen для генерации триангуляций, хотя для настройки требуется немного работы.
