Что такое алгоритм A *, если эвристическая функция H не монотонна?
Я попытался выяснить, каким будет алгоритм A * в случае, если эвристическая функция не удовлетворяет условию монотонности, где в
ч (и) <= e (u, v) + h (v), для любого u, v такого, что между u и v существует ребро
является условием монотонности, где h — эвристическая функция, u и v — вершины в графе поиска, а функция e задает стоимость ребра между u и v (граф поиска является ненаправленным). Тем не менее, википедия (здесь) не дает алгоритм для этого, а также другие источники, такие как книга Norvig по искусственному интеллекту.
Есть хороший источник для изучения этого. Псевдокод был бы великолепен!
Кроме того, я не хочу решать это путем преобразования немонотонной эвристической функции в эвристическую.
Решение
Предполагая, что функция эвристической функции все еще допустимый — * Алгоритм будет работать нормально.
Однако для немонотонных эвристических функций вам может потребоваться обновить уже «закрытый» узел, и вы должны разрешить это поведение.
Другие решения
В случае поиск дерева не обязательно быть последовательным, чтобы быть оптимальным. Вместо этого, если это Поиск граф A * оптимально только в том случае, если эвристика допустима и согласована.
На этом рисунке вы видите пример несогласованной эвристики: алгоритм A * не находит правильный путь.
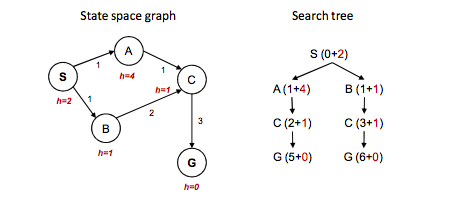
Возможно, вы можете изменить стандартный алгоритм A *, как сказал @amit, но в этом случае вам нужно учитывать уже закрытое состояние, поэтому поиск не будет оптимальным. Он может найти оптимальный путь, но он расширит больше узлов, чем в решении, с согласованной эвристикой, поэтому он будет неоптимальным.
