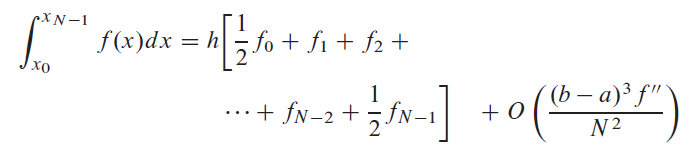Численное интегрирование в переполнении стека

Question

Численное интегрирование в переполнении стека

Мне нужно интегрировать функцию (из двух переменных).
Я знаю, что могу сделать это с помощью Теорема Фубини интегрировать функции одной переменной, затем с использованием численных методов, таких как Прямоугольный метод или Трапециевидное правило.

Но есть ли какие-то встроенные функции, чтобы сделать это в C ++? Мне нужно интегрировать через единицу R2 треугольник ((0,0), (1,0), (0,1)),

4

c++integration numerical

Решение

Другие решения

Насколько я знаю, в стандартной библиотеке нет функций того типа, которые вы ищете. Вот одна из реализаций:

Расширенное трапециевидное правило.

Для фиксированной функции f(x) быть интегрированным между фиксированным
пределы a а также bможно увеличить число интервалов в расширенном трапециевидном правиле вдвое, не теряя преимущества предыдущей работы. Самая грубая реализация правила трапеции состоит в усреднении функции в ее конечных точках. a а также b, Первым этапом уточнения является добавление к этому среднему значению значения функции на полпути. Второй этап уточнения заключается в добавлении значений на 1/4 а также 3/4 точки.

Ряд элементарных квадратурных алгоритмов включает добавление
последовательные этапы уточнения. Удобно заключить эту функцию в Quadrature состав:

struct Quadrature
{
//Abstract base class for elementary quadrature algorithms.
Int n; // Current level of refinement.

virtual Doub next() = 0;
//Returns the value of the integral at the nth stage of refinement.
//The function next() must be defined in the derived class.
};

Тогда Trapzd Структура получается из этого следующим образом:

template<class T>
struct Trapzd: Quadrature
{
Doub a, b, s; // Limits of integration and current value of integral.
T &func;

Trapzd() { };

// func is function or functor to be integrated between limits: a and b
Trapzd(T &funcc, const Doub aa, const Doub bb)
: func(funcc), a(aa), b(bb)
{
n = 0;
}

// Returns the nth stage of refinement of the extended trapezoidal rule.
// On the first call (n = 1), the routine returns the crudest estimate
// of integral of f x / dx in [a,b]. Subsequent calls set n=2,3,... and
// improve the accuracy by adding 2n - 2 additional interior points.
Doub next()
{
Doub x, tnm, sum, del;
Int it, j;
n++;

if (n == 1)
{
return (s = 0.5 * (b-a) * (func(a) + func(b)));
}
else
{
for (it = 1, j = 1; j < n - 1; j++)
{
it <<= 1;
}
tnm = it;
// This is the spacing of the points to be added.
del = (b - a) / tnm;
x = a + 0.5 * del;

for (sum = 0.0,j = 0; j < it; j++, x += del)
{
sum += func(x);
}
// This replaces s by its refined value.
s = 0.5 * (s + (b - a) * sum / tnm);
return s;
}
}
};

Использование:

Trapzd Структура может быть использована несколькими способами.
Самый простой и грубый — интегрировать функцию по расширенному правилу трапеции, где вы заранее знаете, сколько шагов вы хотите. если ты
хочу 2^M + 1Вы можете сделать это фрагментом:

Ftor func;      // Functor func here has no parameters.
Trapzd<Ftor> s(func, a, b);
for(j = 1 ;j <= m + 1; j++) val = s.next();

с ответом, возвращенным как val, Вот Ftor это функтор, содержащий функцию для интеграции.

Бонус:

Конечно, гораздо лучше уточнить правило трапеции до тех пор, пока
степень точности была достигнута. Функция для этого:

template<class T>
Doub qtrap(T &func, const Doub a, const Doub b, const Doub eps = 1.0e-10)
{
// Returns the integral of the function or functor func from a to b.
// The constants EPS can be set to the desired fractional accuracy and
// JMAX so that 2 to the power JMAX-1 is the maximum allowed number of
// steps. Integration is performed by the trapezoidal rule.

const Int JMAX = 20;
Doub s, olds = 0.0; // Initial value of olds is arbitrary.

Trapzd<T> t(func, a, b);

for (Int j = 0; j < JMAX; j++)
{
s = t.next();

if (j > 5) // Avoid spurious early convergence.
{
if (abs(s - olds) < eps * abs(olds) || (s == 0.0 && olds == 0.0))
{
return s;
}
}
olds = s;
}
throw("Too many steps in routine qtrap");
}

Определения типов.

typedef double Doub;    // 64 - bit floating point
typedef int Int;        // 32 - bit signed integer

4

Я бы порекомендовал гауссовские квадратурные и линейные функции формы:

http://www.mathworks.com/matlabcentral/fileexchange/9230-gaussian-quadrature-for-triangles

http://www.wolframalpha.com/input/?i=gaussian+quadrature+triangle

http://www.cs.rpi.edu/~flaherje/pdf/fea6.pdf

2

Источник

Accepted Answer

Вы можете использовать Научная библиотека GNU, который поддерживает многие функции «численного анализа», включая интеграцию.

Очень просто пример интеграции из руководства всего несколько строк кода:

#include <stdio.h>
#include <math.h>
#include <gsl/gsl_integration.h>

double f (double x, void * params) {
double alpha = *(double *) params;
return log(alpha*x) / sqrt(x);
}

int
main (void)
{
double result, error;
double expected = -4.0;
double alpha = 1.0;
gsl_integration_workspace * w
= gsl_integration_workspace_alloc (1000);

gsl_function F;
F.function = &f;
F.params = &alpha;

gsl_integration_qags (&F, 0, 1, 0, 1e-7, 1000,
w, &result, &error);

printf ("result          = % .18f\n", result);
printf ("exact result    = % .18f\n", expected);
printf ("estimated error = % .18f\n", error);
printf ("actual error    = % .18f\n", result - expected);
printf ("intervals =  %d\n", w->size);

gsl_integration_workspace_free (w);

return 0;
}

6