Численная точность для разности квадратов
в моем коде я часто вычисляю такие вещи, как следующий фрагмент (здесь код C для простоты):
float cos_theta = /* some simple operations; no cosf call! */;
float sin_theta = sqrtf(1.0f - cos_theta * cos_theta); // Option 1
В этом примере игнорируйте, что аргумент квадратного корня может быть отрицательным из-за неточностей. Я исправил это с помощью дополнительных fdimf вызов. Тем не менее, я задавался вопросом, является ли следующее более точным:
float sin_theta = sqrtf((1.0f + cos_theta) * (1.0f - cos_theta)); // Option 2
cos_theta находится между -1 а также +1 так что для каждого выбора будут ситуации, когда я вычитаю похожие числа и таким образом теряю точность, верно? Что является наиболее точным и почему?
Решение
Наиболее точным способом с плавающей точкой, вероятно, будет вычисление как sin, так и cos с использованием одной инструкции x87, fsincos.
Однако, если вам нужно выполнить вычисления вручную, лучше сгруппировать аргументы с одинаковыми значениями. Это означает, что второй вариант является более точным, особенно когда cos_theta близко к 0, где точность важнее всего.
Как статья
Что каждый компьютерщик должен знать об арифметике с плавающей точкой заметки:
Выражение х2 — Y2 еще одна формула, которая демонстрирует катастрофические
отмена. это более точным оценивать его как (x — y) (x + y).
Изменить: это сложнее, чем это. Хотя вышеприведенное в целом верно, (x — y) (x + y) немного менее точный когда x и y имеют очень разные величины, как объясняется в сноске к утверждению:
В этом случае (x — y) (x + y) имеет три ошибки округления, но x2 — Y2 имеет только два, так как ошибка округления совершается при вычислении меньшего из х2 и у2 не влияет на итоговое вычитание.
Другими словами, взяв x — y, x + y и произведение (x — y) (x + y), каждый вводит ошибки округления (3 шага ошибки округления). Икс2, Y2, и вычитание х2 — Y2 также каждый из них вносит ошибки округления, но ошибка округления, полученная путем возведения в квадрат относительно небольшого числа (меньшее из x и y), настолько незначительна, что фактически существует только два шага ошибки округления, что делает разницу квадратов более точной.
Так что вариант 1 на самом деле будет более точным. Это подтверждается Java-тестом dev.brutus.
Другие решения
Я написал небольшой тест. Он рассчитывает ожидаемое значение с двойной точностью. Затем он вычисляет ошибку с вашими настройками. Первый вариант лучше:
Algorithm: FloatTest$1
option 1 error = 3.802792362162126
option 2 error = 4.333273185303996
Algorithm: FloatTest$2
option 1 error = 3.802792362167937
option 2 error = 4.333273185305868
Java-код:
import org.junit.Test;
public class FloatTest {
@Test
public void test() {
testImpl(new ExpectedAlgorithm() {
public double te(double cos_theta) {
return Math.sqrt(1.0f - cos_theta * cos_theta);
}
});
testImpl(new ExpectedAlgorithm() {
public double te(double cos_theta) {
return Math.sqrt((1.0f + cos_theta) * (1.0f - cos_theta));
}
});
}
public void testImpl(ExpectedAlgorithm ea) {
double delta1 = 0;
double delta2 = 0;
for (double cos_theta = -1; cos_theta <= 1; cos_theta += 1e-8) {
double[] delta = delta(cos_theta, ea);
delta1 += delta[0];
delta2 += delta[1];
}
System.out.println("Algorithm: " + ea.getClass().getName());
System.out.println("option 1 error = " + delta1);
System.out.println("option 2 error = " + delta2);
}
private double[] delta(double cos_theta, ExpectedAlgorithm ea) {
double expected = ea.te(cos_theta);
double delta1 = Math.abs(expected - t1((float) cos_theta));
double delta2 = Math.abs(expected - t2((float) cos_theta));
return new double[]{delta1, delta2};
}
private double t1(float cos_theta) {
return Math.sqrt(1.0f - cos_theta * cos_theta);
}
private double t2(float cos_theta) {
return Math.sqrt((1.0f + cos_theta) * (1.0f - cos_theta));
}
interface ExpectedAlgorithm {
double te(double cos_theta);
}
}
Кроме того, у вас всегда будет проблема, когда тета мала, потому что косинус плоский вокруг тета = 0. Если тета находится в диапазоне от -0,0001 до 0,0001, то cos (тета) в float равно единице, поэтому ваша sin_theta будет точно равна нуль.
Чтобы ответить на ваш вопрос, когда cos_theta близка к единице (соответствует небольшой тэте), ваше второе вычисление явно более точное. Это показано в следующей программе, которая перечисляет абсолютные и относительные ошибки для обоих вычислений для различных значений cos_theta. Ошибки вычисляются путем сравнения со значением, которое вычисляется с точностью до 200 бит, с использованием библиотеки GNU MP, а затем преобразуется в число с плавающей запятой.
#include <math.h>
#include <stdio.h>
#include <gmp.h>
int main()
{
int i;
printf("cos_theta abs (1) rel (1) abs (2) rel (2)\n\n");
for (i = -14; i < 0; ++i) {
float x = 1 - pow(10, i/2.0);
float approx1 = sqrt(1 - x * x);
float approx2 = sqrt((1 - x) * (1 + x));
/* Use GNU MultiPrecision Library to get 'exact' answer */
mpf_t tmp1, tmp2;
mpf_init2(tmp1, 200); /* use 200 bits precision */
mpf_init2(tmp2, 200);
mpf_set_d(tmp1, x);
mpf_mul(tmp2, tmp1, tmp1); /* tmp2 = x * x */
mpf_neg(tmp1, tmp2); /* tmp1 = -x * x */
mpf_add_ui(tmp2, tmp1, 1); /* tmp2 = 1 - x * x */
mpf_sqrt(tmp1, tmp2); /* tmp1 = sqrt(1 - x * x) */
float exact = mpf_get_d(tmp1);
printf("%.8f %.3e %.3e %.3e %.3e\n", x,
fabs(approx1 - exact), fabs((approx1 - exact) / exact),
fabs(approx2 - exact), fabs((approx2 - exact) / exact));
/* printf("%.10f %.8f %.8f %.8f\n", x, exact, approx1, approx2); */
}
return 0;
}
Выход:
cos_theta abs (1) rel (1) abs (2) rel (2)
0.99999988 2.910e-11 5.960e-08 0.000e+00 0.000e+00
0.99999970 5.821e-11 7.539e-08 0.000e+00 0.000e+00
0.99999899 3.492e-10 2.453e-07 1.164e-10 8.178e-08
0.99999684 2.095e-09 8.337e-07 0.000e+00 0.000e+00
0.99998999 1.118e-08 2.497e-06 0.000e+00 0.000e+00
0.99996835 6.240e-08 7.843e-06 9.313e-10 1.171e-07
0.99989998 3.530e-07 2.496e-05 0.000e+00 0.000e+00
0.99968380 3.818e-07 1.519e-05 0.000e+00 0.000e+00
0.99900001 1.490e-07 3.333e-06 0.000e+00 0.000e+00
0.99683774 8.941e-08 1.125e-06 7.451e-09 9.376e-08
0.99000001 5.960e-08 4.225e-07 0.000e+00 0.000e+00
0.96837723 1.490e-08 5.973e-08 0.000e+00 0.000e+00
0.89999998 2.980e-08 6.837e-08 0.000e+00 0.000e+00
0.68377221 5.960e-08 8.168e-08 5.960e-08 8.168e-08
Когда cos_theta не близко к единице, то точность обоих методов очень близка друг к другу и к ошибке округления.
Правильный способ рассуждать о числовой точности некоторых выражений заключается в следующем:
- Измерьте несоответствие результата относительно правильного значения в ULPs (Блок на последнем месте), введенный в 1960 г. У. Х. Каханом. Вы можете найти C, Python & Mathematica реализации Вот, и узнать больше по теме Вот.
- Различайте два или более выражений на основе их наихудшего случая, а не средней абсолютной ошибки, как в других ответах, или по какой-либо другой произвольной метрике. Так строятся полиномы числовой аппроксимации (Алгоритм Ремеза) как анализируются реализации стандартных библиотечных методов (например, Intel atan2), так далее…
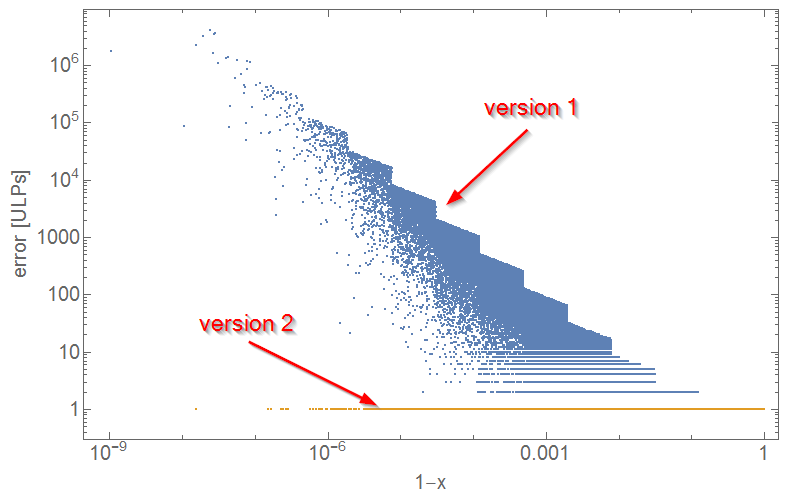
Имея это в виду, version_1: sqrt (1 — x * x) и version_2: sqrt ((1 — x) * (1 + x)) дают значительно разные результаты. Как показано на графике ниже, version_1 демонстрирует катастрофическую производительность для x, близкого к 1, с ошибкой> 1_000_000 ulps, тогда как с другой стороны ошибка version_2 ведется хорошо.
Вот почему я всегда рекомендую использовать version_2, то есть использовать формулу разности квадратов.
Код Python 3.6, который создает файл square_diff_error.csv:
from fractions import Fraction
from math import exp, fabs, sqrt
from random import random
from struct import pack, unpackdef ulp(x):
"""Computing ULP of input double precision number x exploiting
lexicographic ordering property of positive IEEE-754 numbers.
The implementation correctly handles the special cases:
- ulp(NaN) = NaN
- ulp(-Inf) = Inf
- ulp(Inf) = Inf
Author: Hrvoje Abraham
Date: 11.12.2015
Revisions: 15.08.2017
26.11.2017
MIT License https://opensource.org/licenses/MIT
:param x: (float) float ULP will be calculated for
:returns: (float) the input float number ULP value
"""
# setting sign bit to 0, e.g. -0.0 becomes 0.0
t = abs(x)
# converting IEEE-754 64-bit format bit content to unsigned integer
ll = unpack('Q', pack('d', t))[0]
# computing first smaller integer, bigger in a case of ll=0 (t=0.0)
near_ll = abs(ll - 1)
# converting back to float, its value will be float nearest to t
near_t = unpack('d', pack('Q', near_ll))[0]
# abs takes care of case t=0.0
return abs(t - near_t)with open('e:/square_diff_error.csv', 'w') as f:
for _ in range(100_000):
# nonlinear distribution of x in [0, 1] to produce more cases close to 1
k = 10
x = (exp(k) - exp(k * random())) / (exp(k) - 1)
fx = Fraction(x)
correct = sqrt(float(Fraction(1) - fx * fx))
version1 = sqrt(1.0 - x * x)
version2 = sqrt((1.0 - x) * (1.0 + x))
err1 = fabs(version1 - correct) / ulp(correct)
err2 = fabs(version2 - correct) / ulp(correct)
f.write(f'{x},{err1},{err2}\n')
Код Mathematica, который производит окончательный сюжет:
data = Import["e:/square_diff_error.csv"];
err1 = {1 - #[[1]], #[[2]]} & /@ data;
err2 = {1 - #[[1]], #[[3]]} & /@ data;
ListLogLogPlot[{err1, err2}, PlotRange -> All, Axes -> False, Frame -> True,
FrameLabel -> {"1-x", "error [ULPs]"}, LabelStyle -> {FontSize -> 20}]
0.000001 например, опция 1 вернет синус как 1, тогда как опция вернет число чуть меньше 1.
В моем варианте нет разницы, поскольку (1-x) сохраняет точность, не влияющую на переносимый бит. Тогда для (1 + x) то же самое верно. Тогда единственное, что влияет на точность переносимого бита, — это умножение. Таким образом, в обоих случаях существует одно умножение, поэтому они оба с одинаковой вероятностью дают одну и ту же ошибку переноса бита.