C ++ Pattern Matching с кросс-корреляцией FFT (изображения)
всем, кому я пытаюсь реализовать сопоставление с помощью FFT, но я не уверен, каким должен быть результат (я думаю, что что-то упустил, хотя прочитал много материала о проблеме и перепробовал много разных реализаций, этот вариант лучший до сих пор). Вот моя корреляционная функция БПФ.
void fft2d(fftw_complex**& a, int rows, int cols, bool forward = true)
{
fftw_plan p;
for (int i = 0; i < rows; ++i)
{
p = fftw_plan_dft_1d(cols, a[i], a[i], forward ? FFTW_FORWARD : FFTW_BACKWARD, FFTW_ESTIMATE);
fftw_execute(p);
}
fftw_complex* t = (fftw_complex*)fftw_malloc(rows * sizeof(fftw_complex));
for (int j = 0; j < cols; ++j)
{
for (int i = 0; i < rows; ++i)
{
t[i][0] = a[i][j][0];
t[i][1] = a[i][j][1];
}
p = fftw_plan_dft_1d(rows, t, t, forward ? FFTW_FORWARD : FFTW_BACKWARD, FFTW_ESTIMATE);
fftw_execute(p);
for (int i = 0; i < rows; ++i)
{
a[i][j][0] = t[i][0];
a[i][j][1] = t[i][1];
}
}
fftw_free(t);
}
int findCorrelation(int argc, char* argv[])
{
BMP bigImage;
BMP keyImage;
BMP result;
RGBApixel blackPixel = { 0, 0, 0, 1 };
const bool swapQuadrants = (argc == 4);
if (argc < 3 || argc > 4) {
cout << "correlation img1.bmp img2.bmp" << endl;
return 1;
}
if (!keyImage.ReadFromFile(argv[1])) {
return 1;
}
if (!bigImage.ReadFromFile(argv[2])) {
return 1;
}
//Preparations
const int maxWidth = std::max(bigImage.TellWidth(), keyImage.TellWidth());
const int maxHeight = std::max(bigImage.TellHeight(), keyImage.TellHeight());
const int rowsCount = maxHeight;
const int colsCount = maxWidth;
BMP bigTemp = bigImage;
BMP keyTemp = keyImage;
keyImage.SetSize(maxWidth, maxHeight);
bigImage.SetSize(maxWidth, maxHeight);
for (int i = 0; i < rowsCount; ++i)
for (int j = 0; j < colsCount; ++j) {
RGBApixel p1;
if (i < bigTemp.TellHeight() && j < bigTemp.TellWidth()) {
p1 = bigTemp.GetPixel(j, i);
} else {
p1 = blackPixel;
}
bigImage.SetPixel(j, i, p1);
RGBApixel p2;
if (i < keyTemp.TellHeight() && j < keyTemp.TellWidth()) {
p2 = keyTemp.GetPixel(j, i);
} else {
p2 = blackPixel;
}
keyImage.SetPixel(j, i, p2);
}
//Here is where the transforms begin
fftw_complex **a = (fftw_complex**)fftw_malloc(rowsCount * sizeof(fftw_complex*));
fftw_complex **b = (fftw_complex**)fftw_malloc(rowsCount * sizeof(fftw_complex*));
fftw_complex **c = (fftw_complex**)fftw_malloc(rowsCount * sizeof(fftw_complex*));
for (int i = 0; i < rowsCount; ++i) {
a[i] = (fftw_complex*)fftw_malloc(colsCount * sizeof(fftw_complex));
b[i] = (fftw_complex*)fftw_malloc(colsCount * sizeof(fftw_complex));
c[i] = (fftw_complex*)fftw_malloc(colsCount * sizeof(fftw_complex));
for (int j = 0; j < colsCount; ++j) {
RGBApixel p1;
p1 = bigImage.GetPixel(j, i);
a[i][j][0] = (0.299*p1.Red + 0.587*p1.Green + 0.114*p1.Blue);
a[i][j][1] = 0.0;
RGBApixel p2;
p2 = keyImage.GetPixel(j, i);
b[i][j][0] = (0.299*p2.Red + 0.587*p2.Green + 0.114*p2.Blue);
b[i][j][1] = 0.0;
}
}
fft2d(a, rowsCount, colsCount);
fft2d(b, rowsCount, colsCount);
result.SetSize(maxWidth, maxHeight);
for (int i = 0; i < rowsCount; ++i)
for (int j = 0; j < colsCount; ++j) {
fftw_complex& y = a[i][j];
fftw_complex& x = b[i][j];
double u = x[0], v = x[1];
double m = y[0], n = y[1];
c[i][j][0] = u*m + n*v;
c[i][j][1] = v*m - u*n;
int fx = j;
if (fx>(colsCount / 2)) fx -= colsCount;
int fy = i;
if (fy>(rowsCount / 2)) fy -= rowsCount;
float r2 = (fx*fx + fy*fy);
const double cuttoffCoef = (maxWidth * maxHeight) / 37992.;
if (r2<128 * 128 * cuttoffCoef)
c[i][j][0] = c[i][j][1] = 0;
}
fft2d(c, rowsCount, colsCount, false);
const int halfCols = colsCount / 2;
const int halfRows = rowsCount / 2;
if (swapQuadrants) {
for (int i = 0; i < halfRows; ++i)
for (int j = 0; j < halfCols; ++j) {
std::swap(c[i][j][0], c[i + halfRows][j + halfCols][0]);
std::swap(c[i][j][1], c[i + halfRows][j + halfCols][1]);
}
for (int i = halfRows; i < rowsCount; ++i)
for (int j = 0; j < halfCols; ++j) {
std::swap(c[i][j][0], c[i - halfRows][j + halfCols][0]);
std::swap(c[i][j][1], c[i - halfRows][j + halfCols][1]);
}
}
for (int i = 0; i < rowsCount; ++i)
for (int j = 0; j < colsCount; ++j) {
const double& g = c[i][j][0];
RGBApixel pixel;
pixel.Alpha = 0;
int gInt = 255 - static_cast<int>(std::floor(g + 0.5));
pixel.Red = gInt;
pixel.Green = gInt;
pixel.Blue = gInt;
result.SetPixel(j, i, pixel);
}BMP res;
res.SetSize(maxWidth, maxHeight);
result.WriteToFile("result.bmp");
return 0;
}
Образец вывода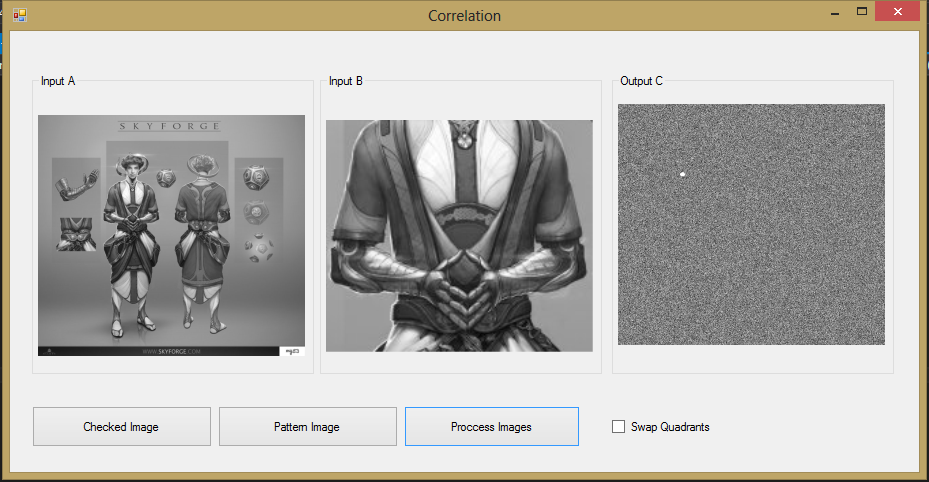
Решение
Этот вопрос, вероятно, будет более уместно размещен на другом сайте, как перекрестная проверка (metaoptimize.com раньше тоже был хорошим, но, похоже, его уже нет)
Это говорит:
Есть две аналогичные операции, которые вы можете выполнять с помощью БПФ: свертка и корреляция. Свертка используется для определения того, как два сигнала взаимодействуют друг с другом, тогда как корреляция может использоваться для выражения того, насколько похожи два сигнала друг на друга. Убедитесь, что вы делаете правильную операцию, так как они обычно реализуются через DFT.
Для такого типа применения ДПФ вы обычно не извлекаете какую-либо полезную информацию в спектре Фурье, если вы не искали частоты, общие для обоих источников данных или чего-либо еще (например, если вы сравнивали два моста, чтобы увидеть, расположены ли их опоры одинаково. ).
Ваше третье изображение очень похоже на домен власти; обычно я вижу корреляцию полностью серой, за исключением случаев, когда произошло наложение. Ваш код определенно вычисляет обратный ДПФ, поэтому, если я не пропущу что-то, единственным другим объяснением, которое я придумаю для нечеткого вида, могут быть некоторые из кода «фактора выдумки», например:
if (r2<128 * 128 * cuttoffCoef)
c[i][j][0] = c[i][j][1] = 0;
Что касается того, что вы должны ожидать: там, где есть общие элементы между двумя изображениями, вы увидите пик. Чем больше пик, тем больше сходство двух изображений вблизи этой области.
Некоторые комментарии и / или рекомендуемые изменения:
1) свертка & корреляции не являются масштабно-инвариантными операциями. Другими словами, размер изображения шаблона может существенно повлиять на ваш результат.
2) Нормализовать ваши изображения до корреляции.
Когда вы получите данные изображения, готовые для прямого прохода DFT:
a[i][j][0] = (0.299*p1.Red + 0.587*p1.Green + 0.114*p1.Blue);
a[i][j][1] = 0.0;
/* ... */
Как вы серого изображения это ваше дело (хотя я бы выбрал что-то вроде sqrt( r*r + b*b + g*g )). Тем не менее, я не вижу, что вы делаете что-то для нормализации изображения.
Слово «нормализовать» может иметь несколько разных значений в этом контексте. Два распространенных типа:
- нормализовать диапазон значений от 0,0 до 1,0
- нормализовать «белизну» изображений
3) Проведите ваше изображение шаблона через фильтр улучшения края. Я лично использовал себе на уме, Собела, и я думаю, что я перепутал с несколькими другими. Насколько я помню, canny был «быстрым и грязным», sobel был дороже, но я получил сопоставимые результаты, когда пришло время сделать корреляцию. Увидеть глава 24 книги «dsp guide», которая свободно доступна онлайн. Вся книга стоит вашего времени, но если у вас мало времени, то как минимум глава 24 очень поможет.
4) Измените масштаб выходного изображения между [0, 255]; если вы хотите реализовать пороговые значения, сделайте это после этого шага, потому что шаг порогового значения с потерями.
Моя память об этом туманна, но, насколько я помню, (отредактировано для ясности):
- Вы можете масштабировать конечные пиксели изображения (до масштабирования) между [-1,0, 1,0], отделяя наибольшее значение спектра мощности от всего спектра мощности
- Наибольшее значение спектра мощности, что достаточно удобно, является самым центральным значением в спектре мощности (соответствует самой низкой частоте)
- Если вы разделите его на спектр мощности, вы в конечном итоге сделаете вдвое больше работы; поскольку БПФ линейны, вы можете отложить деление до тех пор, пока не пройдет обратный переход ДПФ, до повторного масштабирования пикселей между [0..255].
- Если после пересчета большинство ваших значений окажется таким черным, что вы их не увидите, вы можете использовать решение для ODE
y' = y(1 - y)(Одним из примеров является сигмовиднаяf(x) = 1 / (1 + exp(-c*x) )для некоторого коэффициента масштабированияcэто дает лучшие градации). Это больше связано с улучшением вашей способности интерпретировать результаты визуально, чем с чем-либо, что вы можете использовать для программного поиска пиков.
редактировать Я сказал [0, 255] выше. Я предлагаю вам изменить масштаб на [128, 255] или другую нижнюю границу, которая скорее серая, чем черная.
Другие решения
