Быстрый способ выяснить, важен ли край для подключения графов
У меня есть набор ребер E, и я хочу знать, могу ли я безопасно удалить ребро i в E, то есть, если я удалю его из графа, граф все равно должен быть соединен.
В моем понимании это подразумевает, что ребро i должно лежать на окружности.
Вывод должен быть списком индексов всех ребер, которые я не могу удалить.
Эта проблема:
Мои разные решения кажутся правильными, но слишком медленными (неэффективными).
Одним из моих решений было:
1. Loop through all edges i in E
2. Loop through all edges x in V
3. Add edge x to the graph (excluding edge i) until nodes of i are connected or end reached
4. If no connection possible, edge is not removable and added to the list
Этот путь был слишком медленным.
Затем я решил переписать свой код и использовать поиск в ширину, чтобы посмотреть, возможен ли другой путь без ребра i.
Я думал, что это будет достаточно производительным, но, похоже, это не так. Либо я реализовал очень плохо, либо это также неправильный алгоритм для этой задачи.
Вот алгоритм в коде C ++, который у меня есть (удалены некоторые не важные части):
struct connection {
int a, b;
};
void expand(int x, connection *&arr, std::set<int> &exp, int size) {
for (int i = 0; i < size; i++) {
if (x == arr[i].a) {
exp.insert(arr[i].b);
}
else if (x == arr[i].b) {
exp.insert(arr[i].a);
}
}
return;
}
// recursive breadth-first-seach
bool BFSr(std::set<int> &group, std::set<int> &visited, int goal, connection *&arr, int size) {
if (group.empty()) return false;
if (group.find(goal) != group.end()) return true;
std::set<int> tempa;
for (std::set<int>::iterator it = group.begin(); it != group.end(); ++it) {
expand(*it, arr, tempa size);
}
for (std::set<int>::iterator it = visited.begin(); it != visited.end(); ++it) {
tempa.erase(*it);
}
tempb = visited;
tempb.insert(group.begin(), group.end());
return BFSr(tempa, tempb, goal, arr, size);
}
bool BFS(int start, int goal, connection *&arr, int size) {
std::set<int> tempa;
std::set<int> tempb;
tempa.insert(start);
return BFSr(tempa, tempb, goal, arr, size);
}
int main()
{
connection *arr = new connection[m];
connection *con = new connection[m - 1];
// fill arr with connections arr.a < arr.b ....
for (int j = 0; j < (m - 1); j++) {
con[j] = arr[j + 1];
}
// 1. edge for performance reasons extra
if (!BFS(arr[0].a, arr[0].b, con, (m - 1))) {
// connection is important therefore add to list
printf(" %d", 1);
}
// Look if nodes still connected after removing connection
for (int s = 1; s < m; s++) {
con[s - 1] = arr[s - 1];
if (!BFS(arr[s].a, arr[s].b, con, (m-1))) {
// connection is important therefore add to list
printf(" %d", s + 1);
}
}
printf("\n");free(arr);
free(con);
return 0;
}
Знаете ли вы какие-либо решения для меня, чтобы сделать это быстрее, или вы знаете лучший алгоритм для моей проблемы?
Решение
Ребро, удаление которого разъединяет два соединенных компонента, называется мост и существуют алгоритмы линейного времени для нахождения всех мостов в графе (обычно основанные на поиске в глубину). В статье Википедии приведен один из них (из-за Тарьяна) в качестве примера. Эта бумага также дает простой алгоритм для перечисления всех мостов в графе и кажется немного проще, чем алгоритм Тарьяна.
Надеюсь это поможет!
Другие решения
Вот еще одна версия вашего алгоритма (я полагаю, вы получите бесплатную реализацию графического стандарта и различные алгоритмы оптимизации):
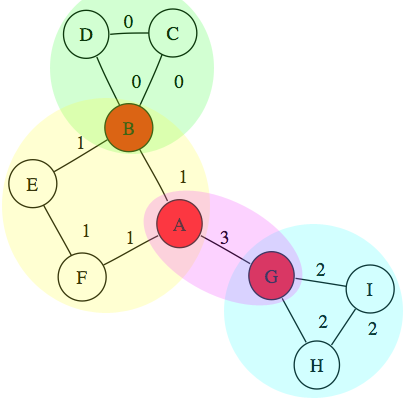
Я имею в виду это изображение как модель графа.
Гист (из этого сообщение)
- найти точки сочленения
- все точки с одним выходом
точки сочленения (график повышения не возвращает их) — эти ребра
автоматически соединяют края - для каждой точки сочленения-
зацикливайтесь на каждом выходном элементе, если выходной элемент уже не перекрывает ребро, тогда
удалите ребро и проверьте компоненты графа и добавьте ребро обратно
снова
В конце он напечатает Край (a, g) соединяет компоненты в графе
#include <iostream>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/biconnected_components.hpp>
#include <boost/graph/connected_components.hpp>
#include <functional>
#include <string>
#include <vector>
#include <unordered_map>
#include <unordered_set>
typedef boost::adjacency_list <boost::vecS, boost::vecS, boost::undirectedS> Graph;
typedef boost::graph_traits<Graph>::vertex_descriptor vertex_t;
typedef boost::graph_traits<Graph>::edge_descriptor edge_t;
// reference:
// http://lists.boost.org/boost-users/2005/08/13098.php
//
struct edge_t_hasher
{
std::size_t operator()(const edge_t& e) const
{
auto prop = e.get_property();
std::hash<decltype(prop)> hasher;
return hasher(prop);
}
};
typedef std::unordered_set<edge_t, edge_t_hasher> UnorderedBoostEdgeSet;
Graph getGraph()
{
Graph g;
vertex_t aVtx = boost::add_vertex(g);
vertex_t bVtx = boost::add_vertex(g);
vertex_t cVtx = boost::add_vertex(g);
vertex_t dVtx = boost::add_vertex(g);
vertex_t eVtx = boost::add_vertex(g);
vertex_t fVtx = boost::add_vertex(g);
vertex_t gVtx = boost::add_vertex(g);
vertex_t hVtx = boost::add_vertex(g);
vertex_t iVtx = boost::add_vertex(g);
boost::add_edge(dVtx, cVtx, g);
boost::add_edge(dVtx, bVtx, g);
boost::add_edge(cVtx, bVtx, g);
boost::add_edge(aVtx, bVtx, g);
boost::add_edge(bVtx, eVtx, g);
boost::add_edge(eVtx, fVtx, g);
boost::add_edge(aVtx, fVtx, g);
boost::add_edge(aVtx, gVtx, g);// edge connecting components
boost::add_edge(gVtx, iVtx, g);
boost::add_edge(gVtx, hVtx, g);
boost::add_edge(hVtx, iVtx, g);
return g;
}
UnorderedBoostEdgeSet bridgingEdgesForGraph(const Graph& graph)
{
UnorderedBoostEdgeSet bridgeEdges;
std::unordered_set<vertex_t> articulationVertices;
boost::articulation_points(graph, std::inserter(articulationVertices, articulationVertices.end()));
// add all the single connected vertices to the articulation vertices
auto vtxIters = boost::vertices(graph);
for (auto it = vtxIters.first, end = vtxIters.second; it != end; ++it)
{
if (boost::out_degree(*it, graph) == 1)
bridgeEdges.insert(*(boost::out_edges(*it, graph).first));
}
std::vector<vertex_t> componentsInGraph(boost::num_vertices(graph));
int numComponentsInGraph = boost::connected_components(graph, &componentsInGraph[0]);
// for each articulation vertex now get edges and check if removing that
// edge causes graph change in connected components
//
// copy the graph- so we can iterate over the outeges of vertices
// we will be fiddling with the copy- since the vtx descriptors are
// ints- they stay same across copy and removing edge operation
auto graph2 = graph;
for (auto vtx : articulationVertices)
{
auto outEdges = boost::out_edges(vtx, graph);
for (auto it = outEdges.first, end = outEdges.second; it != end; ++it)
{
auto edge = *it;
if (bridgeEdges.find(edge) != bridgeEdges.end())
continue;
// map this edge to graph2 edge- for removal and eventual addition
auto src = boost::source(edge, graph);
auto tgt = boost::target(edge, graph);
auto edge2 = boost::edge(src, tgt, graph2).first;
boost::remove_edge(edge2, graph2);
std::vector<vertex_t> componentsInGraph2(boost::num_vertices(graph2));
int numComponentsInGraph2 = boost::connected_components(graph2, &componentsInGraph2[0]);
// bridging edge- graph #components changed
if (numComponentsInGraph != numComponentsInGraph2)
bridgeEdges.insert(edge);
// add the edge back to graph2
boost::add_edge(src, tgt, graph2);
}
}
return bridgeEdges;
}
int main()
{
const Graph& graph = getGraph();
const auto& bridgingEdges = bridgingEdgesForGraph(graph);
const char* array = {"ABCDEFGHI"};
for (auto edge : bridgingEdges)
{
std::cout << "Edge(" << array[boost::source(edge, graph)] << ", " << array[boost::target(edge, graph)]
<< ") is a bridging edge" << std::endl;
}
return 0;
}
Тем временем я узнал, как называются эти особые ребра: Мосты.
И поэтому я нашел сайт, предоставляющий алгоритм DFS для нахождения всех мостов.
Это достаточно быстро для моих целей.
Алгоритм DFS для нахождения мостов в неориентированном графе
Спасибо Sarang, ваш пост заставил меня найти правильные слова для поиска по сайту.
