Быстрое целочисленное решение x (x-1) / 2 = c
Учитывая неотрицательное целое число cМне нужен эффективный алгоритм, чтобы найти наибольшее целое число x такой, что
x*(x-1)/2 <= c
Аналогично, мне нужен эффективный и надежно точный алгоритм для вычисления:
x = floor((1 + sqrt(1 + 8*c))/2) (1)
Для определенности я пометил этот вопрос C ++, поэтому ответом должна быть функция, написанная на этом языке. Вы можете предположить, что c является 32-битным целым без знака
Кроме того, если вы можете доказать, что (1) (или эквивалентное выражение, включающее арифметику с плавающей точкой) всегда дает правильный результат, это тоже правильный ответ, так как с плавающей точкой на современных процессорах может быть быстрее, чем целочисленные алгоритмы.
Решение
Если вы хотите предположить, что IEEE удваивается с правильным округлением для всех операций, включая квадратный корень, то написанное вами выражение (плюс приведение к двойному) дает правильный ответ на все входные данные.
Вот неофициальное доказательство. поскольку c 32-разрядное целое число без знака, преобразуемое в тип с плавающей точкой с 53-разрядным значением, 1 + 8*(double)c точно, и sqrt(1 + 8*(double)c) правильно округлено. 1 + sqrt(1 + 8*(double)c) с точностью до одного ульпа, так как последний член меньше 2**((32 + 3)/2) = 2**17.5 подразумевает, что единица в последнем месте последнего термина меньше 1, и поэтому (1 + sqrt(1 + 8*(double)c))/2 с точностью до одного ульпа, так как деление на 2 это точно.
Последняя часть бизнеса — это слово. Проблемные случаи здесь, когда (1 + sqrt(1 + 8*(double)c))/2 округляется до целого числа. Это происходит тогда и только тогда, когда sqrt(...) округляет до нечетного целого числа. Поскольку аргумент sqrt целое число, худшие случаи выглядят как sqrt(z**2 - 1) для положительных нечетных целых zи мы связаны
z - sqrt(z**2 - 1) = z * (1 - sqrt(1 - 1/z**2)) >= 1/(2*z)
расширением Тейлора. поскольку z меньше чем 2**17.5, разрыв до ближайшего целого не менее 1/2**18.5 в результате величины меньше, чем 2**17.5Это означает, что эта ошибка не может быть результатом правильно округленной sqrt,
Приняв упрощение Якка, мы можем написать
(uint32_t)(0.5 + sqrt(0.25 + 2.0*c))
без дальнейшей проверки.
Другие решения
Если мы начнем с квадратной формулы, мы быстро достигнем sqrt(1/4 + 2c)округлите до 1/2 или выше.
Теперь, если вы делаете этот расчет с плавающей запятой, могут быть неточности.
Существует два подхода к устранению этих неточностей. Во-первых, нужно тщательно определить, насколько они велики, определить, достаточно ли рассчитанное значение близко к половине, чтобы они были важны. Если они не важны, просто верните значение. Если это так, мы все равно можем связать ответ одним из двух значений. Проверьте эти два значения в целочисленной математике и верните.
Тем не менее, мы можем покончить с этим осторожным и заметить, что sqrt(1/4 + 2c) будет иметь ошибку меньше, чем 0.5 если значения 32 бит, и мы используем doubles. (Мы не можем сделать эту гарантию с floatс, как по 2^31 float не выдерживаю +0.5 без округления).
По сути, мы используем квадратную формулу, чтобы уменьшить ее до двух возможностей, а затем протестируем эти две.
uint64_t eval(uint64_t x) {
return x*(x-1)/2;
}
unsigned solve(unsigned c) {
double test = sqrt( 0.25 + 2.*c );
if ( eval(test+1.) <= c )
return test+1.
ASSERT( eval(test) <= c );
return test;
}
Обратите внимание, что преобразование положительного double к целому типу округляет до 0. Вы можете вставить floorЕсли хочешь.
Это может быть немного касательно вашего вопроса. Но то, что привлекло мое внимание, это конкретная формула. Вы пытаетесь найти треугольный корень Tn — 1 (где ТN это N3-е треугольное число).
т.е .:
TN = n * (n + 1) / 2
а также
TN — n = Tn — 1 = n * (n — 1) / 2
Из описанного хитрого трюка Вот, для ТN у нас есть:
n = int (sqrt (2 * c))
Ищу такой что Tn — 1 ≤ c в этом случае не меняет определения n по той же причине, что и в первоначальном вопросе.
В вычислительном отношении это экономит несколько операций, поэтому теоретически быстрее, чем точное решение (1). На самом деле, это примерно то же самое.
Однако ни это решение, ни представленное Дэвидом не являются такими же «точными», как ваше (1).
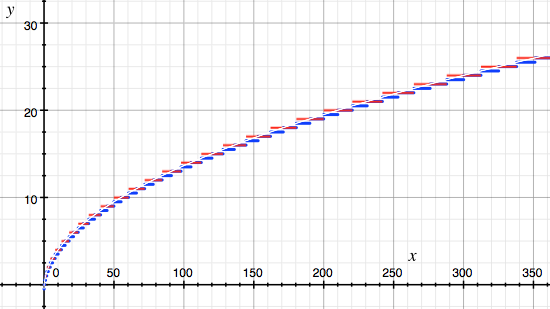
пол ((1 + sqrt (1 + 8 * c)) / 2) (синий) против int (sqrt (2 * c)) (красный) против точного (белая линия)
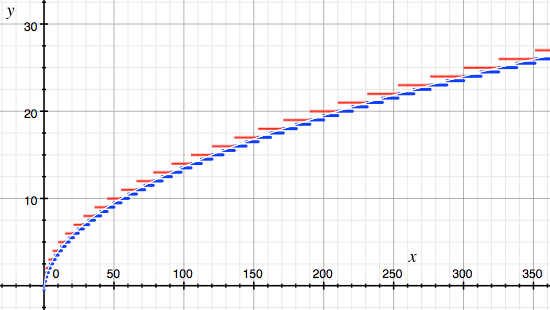
пол ((1 + sqrt (1 + 8 * c)) / 2) (синий) против int (sqrt (0,25 + 2 * c) + 0,5 (красный) против точного (белая линия)
Моя реальная точка зрения в том, что треугольные числа — это забавный набор чисел, которые связаны с квадратами, треугольником Паскаля, числами Фибоначчи и так далее. и др.
Как таковые есть множество личностей вокруг них, которые могут быть использованы для перестановки проблемы таким образом, чтобы не требовался квадратный корень.
Особый интерес может быть то, что TN + Tn — 1 = n2
Я предполагаю, что вы знаете, что работаете с треугольным числом, но если вы этого не поняли, поиск треугольных корней приводит к нескольким вопросам, таким как этот которые по той же теме.