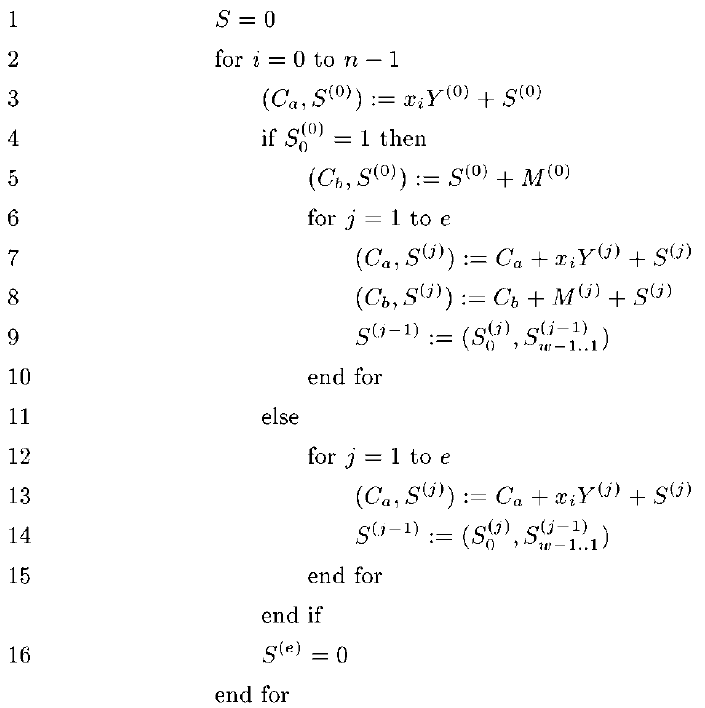Bizzare идентичные неверные результаты в разных алгоритмах MWR2MM для умножения Монтгомери RSA

Я пытаюсь реализовать RSA 2048 в аппаратном обеспечении (xilinx ZYNQ FPGA), используя различные методы Монтгомери. Я реализую алгоритм с использованием Xilinx HLS (по сути код C ++, который синтезируется в аппаратное обеспечение).

Примечание: ради этого поста трактуйте его как стандартную реализацию C ++, за исключением того, что у меня могут быть переменные, которые действуют как битовые векторы шириной до 4096 бит, и доступ к отдельным битам с использованием foo[bit] или же foo.range(7,0) синтаксис. Я еще не распараллелил его, поэтому он должен вести себя так же, как стандартный код C ++. Пожалуйста, не бойтесь и перестаньте читать, потому что я сказал слова FPGA и HLS. Просто относитесь к этому как к коду C ++.

Мне удалось получить работающий прототип, который использует стандартное квадратичное и умножение для модульного возведения в степень и стандартный алгоритм MMX radix-2 для модульного умножения, однако он занимает слишком много места на FPGA, и мне нужно использовать менее ресурсоемкие алгоритмы.

Чтобы сэкономить место, я пытаюсь реализовать Tenka-koc Масштабируемое множественное слово Radix 2 Умножение Монтгомери (MWR2MM) предложил Вот. Я боролся с этим в течение месяца, но безрезультатно. Однако из-за моей борьбы возникает интересная проблема, которую я не могу понять.

Моя проблема в том, что MWR2MM не возвращает правильный ответ при выполнении умножения Монтгомери. Однако я начинаю думать, что это не ошибка кодирования, а, скорее, что я просто неправильно истолковываю что-то критическое в использовании алгоритма.

Существует несколько вариантов алгоритма MWR2MM с довольно разными реализациями, и я попытался реализовать многие из них. В настоящее время у меня есть 4 различных реализации MWR2MM, все они основаны на модификациях алгоритма, изложенных в ряде статей. Что заставляет меня думать, что мои реализации на самом деле верны, так это то, что все эти различные версии алгоритма возвращают один и тот же НЕПРАВИЛЬНЫЙ ответ! Я не думаю, что это совпадение, но я также не думаю, что опубликованные алгоритмы неверны … Поэтому я утверждаю, что на самом деле происходит нечто более гнусное, и мои реализации алгоритмов верны.

Например, возьмите оригинальный предложенный MWR2MM, предложенный в статье tenca-koc, которую мы называем MWR2MM_CSA, потому что все операции сложения алгоритма используют сумматор с переносом-сохранением (CSA) при реализации в аппаратном обеспечении.

• S — частичная сумма
• М — модуль
• Y является мультипликатором
• X — это множитель, а x_i (нижний индекс) — это один бит (например, X = (x_n, …, x_1, x_0).
• Верхний индекс — это векторы слов (например, M = (0, M ^ {e-1}, …, M ^ 1, M ^ 0)
• (A, B) — конкатенация двух битовых векторов.
• м — ширина операндов
• w — ширина выбранных слов
• e — количество w-битных слов, необходимых для заполнения векторов (например, e = ceil ((m + 1) / w))

Моя реализация этого алгоритма использует следующие параметры:

• MWR2MM_m = 2048 (operand size, m from above)
• MWR2MM_w = 8 (word size, w from above)
• MWR2MM_e = ceil( (e+1)/w ) = 257 (number of words + 1 per operand, e from above)
• ap_uint<NUM_BITS> как вы объявляете битовый вектор в HLS

Мой код:

void mwr2mm_csa( ap_uint<MWR2MM_m> X,
ap_uint<MWR2MM_w> Y[MWR2MM_e+1],
ap_uint<MWR2MM_w> M[MWR2MM_e+1],
ap_uint<MWR2MM_m> *out)
{
// Declare and zero partial sum S
ap_uint<MWR2MM_w> S[MWR2MM_e] = 0;
for (int i=0; i<MWR2MM_e; i++)
S[i] = 0;

// Two Carry bits
ap_uint<1> Ca=0, Cb=0;

for (int i=0; i<MWR2MM_m; i++)
{
(Ca,S[0]) = X[i]*Y[0] + S[0]; // this is how HLS concatenates vectors, just like in the paper!
if (S[0][0] == 1) // if the 0th bit of the 0th word is 1
{
(Cb,S[0]) = S[0] + M[0];
for (int j=1; j<=MWR2MM_e; j++)
{
(Ca, S[j]) = Ca + X[i]*Y[j] + S[j];
(Cb, S[j]) = Cb + M[j] + S[j];
S[j-1] = ( S[j][0], S[j-1].range(MWR2MM_w-1,1) );
}
}
else
{
for (int j=1; j<=MWR2MM_e; j++)
{
(Ca, S[j]) = Ca + X[i]*Y[j] + S[j];
S[j-1] = ( S[j][0], S[j-1].range(MWR2MM_w-1,1) );
}
}
}

// copy the result to the output pointer
for (int i=0; i<MWR2MM_e-1; i++)
out->range(MWR2MM_w*i+(MWR2MM_w-1), MWR2MM_w*i) = S[i].to_uchar();
}

Теперь, насколько я понимаю, (цитата из статьи выше)

алгоритм умножения Монтгомери (ММ) на два целых числа X и Y,
с необходимыми параметрами для n битов точности, приведет к
число MM (X, Y, M) = XY(2 ^ -n) (по модулю m), где r = 2 ^ n и M представляет собой
целое число в диапазоне (2 ^ (n-1), 2 ^ (n)), такое что gcd (r, M) = 1. поскольку
r = 2 ^ n, достаточно, чтобы модуль M был нечетным целым числом.

Следовательно, следует ожидать следующих результатов (проверено с помощью библиотеки программного обеспечения):

X = 0xABA5E025B607AA14F7F1B8CC88D6EC01C2D17C536508E7FA10114C9437D9616C9E1C689A4FC54744FA7DFE66D6C2FCF86E332BFD6195C13FE9E331148013987A947D9556A27A326A36C84FB38BFEFA0A0FFA2E121600A4B6AA4F9AD2F43FB1D5D3EB5EABA13D3B382FED0677DF30A089869E4E93943E913D0DC099AA320B8D8325B2FC5A5718B19254775917ED48A34E86324ADBC8549228B5C7BEEEFA86D27A44CEB204BE6F315B138A52EC714888C8A699F6000D1CD5AB9BF261373A5F14DA1F568BE70A0C97C2C3EFF0F73F7EBD47B521184DC3CA932C91022BF86DD029D21C660C7C6440D3A3AE799097642F0507DFAECAC11C2BD6941CBC66CEDEEAB744
Y = 0xD091BE9D9A4E98A172BD721C4BC50AC3F47DAA31522DB869EB6F98197E63535636C8A6F0BA2FD4C154C762738FBC7B38BDD441C5B9A43B347C5B65CFDEF4DCD355E5E6F538EFBB1CC161693FA2171B639A2967BEA0E3F5E429D991FE1F4DE802D2A1D600702E7D517B82BFFE393E090A41F57E966A394D34297842552E15550B387E0E485D81C8CCCAAD488B2C07A1E83193CE757FE00F3252E4BD670668B1728D73830F7AE7D1A4C02E7AFD913B3F011782422F6DE4ED0EF913A3A261176A7D922E65428AE7AAA2497BB75BFC52084EF9F74190D0D24D581EB0B3DAC6B5E44596881200B2CE5D0FB2831D65F036D8E30D5F42BECAB3A956D277E3510DF8CBA9
M = 0xD27BF9F01E2A901DB957879F45F697330D21A21095DA4FA7D3AAB75454A8E9F0F4EA531ECE34F0C3BA9E02EB27D8F0DBE78EEDE4AC84061BEEF162D00B55C0DD772D28F23E994899AA19B9BEA7B12A8027A32A92190A3630E249544675488121565A23548FCD36F5382EEB993DB9CE3F526F20AB355E82D963D59541BC1161E211A03E3B372560840C57E12BD2F40EAC5FFCEC01B3F07C378C0A60B74BEF7B572764C88A4F98B61FA8CCD905AFAE779E6193378304D8EB17695CE71A173AC3DE11271753C48DB58546E5AF9917C1CEBBA5BB1AF3FCE3DF9516C0C95C9BC14BB65D1C53078C06C81AC0F3ED0D8634260E47BF780CF4F4996084DF732935194417
MM(X,Y,M) = 0x444682CC199679928F5971191ACCB8EAA5C76CF743E54FC28FD8DCFF57BD198677A26A5C1A6254810A91049FA85CBE3EDDFDCDF12ED3FBB204DE249C389CDEE3FA6DB65441AFE03F1148660EA0E756E038891CEF098F2A009FB443685202FAC40D8FE7B82A1F643020EA31F5A8F4B253AD2F30028C59F1E2DCF3902BBC48E73ECA7BDC22BB92E8A70BC535584BF644CAF24EF39A1899F18C05937446AACC5C64762AFAD2B73EEDF3AA96C9A4CFF836A551A26AED46279328EDD4B9BBBC182B9E408640D058926882B3A0FAA043F726EF96E07B7960D586E2648534EB15C23FE152D0D088F1742E023715E3ABAEC8128B51CC86E8BC207D69F1E6BA7067D44429

Но вместо этого мой алгоритм возвращает

MWR2MM_csa(X,Y,M) = 0x16C27CBC37C109B048B0F8B860C3501DB2E90F07D9BF9F6A63839453AC6603776C8CBD7AE8974544C52F078AD035AF1AC58CBBD5DB5801CDF3CF876C43F29FC1719ADF46804928D8BB621FCD48988160602C47812299603181FD97AEC74B7BE563EA0B0CB9EC9B2559191D8EE6AE8092FF9E50ADC1B874BC40C9256D785A4920DC1C1A5DF2B8492B181D16841EEA5377524BDF9BCC8A6DC3919DD4FDF6BBD7BB9D8FC35D06D7A4135363A2AA7FA6AE43B335A2704B007E405731A0D5D352EF7C51AD58241D201E07FA86AA395BB8F5AB3C9B966D5DB966777B45FE47B1838B97AFED23907D7AF61CF809D0B934FC3899998BFEF5B11516CA76C62D999CED8840

Хорошо, возможно, эта реализация была неправильной. Давайте попробуем другую модифицированную версию, алгоритм MWR2MM_CPA (названный для сумматоров переноса-пропогата, используемых в аппаратном обеспечении):

И моя реализация MWR2MM_CSA:

void mwr2mm_cpa(rsaSize_t X, rsaSize_t Yin, rsaSize_t Min, rsaSize_t* out)
{
// extend operands to 2 extra words longer
ap_uint<MWR2MM_m+2*MWR2MM_w> Y = Yin;
ap_uint<MWR2MM_m+2*MWR2MM_w> M = Min;
ap_uint<MWR2MM_m+2*MWR2MM_w> S = 0;

ap_uint<2> C = 0;
bit_t qi = 0;

// unlike the previous example, we store the concatenations in a temporary variable
ap_uint<10> temp_concat=0;

for (int i=0; i<MWR2MM_m; i++)
{
qi = (X[i]*Y[0]) xor S[0];

// C gets top two bits of temp_concat, j'th word of S gets bottom 8 bits of temp_concat
temp_concat = X[i]*Y.range(MWR2MM_w-1,0) + qi*M.range(MWR2MM_w-1,0) + S.range(MWR2MM_w-1,0);
C = temp_concat.range(9,8);
S.range(MWR2MM_w-1,0) = temp_concat.range(7,0);

for (int j=1; j<=MWR2MM_e; j++)
{
temp_concat = C + X[i]*Y.range(MWR2MM_w*j+(MWR2MM_w-1), MWR2MM_w*j) + qi*M.range(MWR2MM_w*j+(MWR2MM_w-1), MWR2MM_w*j) + S.range(MWR2MM_w*j+(MWR2MM_w-1), MWR2MM_w*j);
C = temp_concat.range(9,8);
S.range(MWR2MM_w*j+(MWR2MM_w-1), MWR2MM_w*j) = temp_concat.range(7,0);

S.range(MWR2MM_w*(j-1)+(MWR2MM_w-1), MWR2MM_w*(j-1)) = (S.bit(MWR2MM_w*j), S.range( MWR2MM_w*(j-1)+(MWR2MM_w-1), MWR2MM_w*(j-1)+1));
}
S.range(S.length()-1, S.length()-MWR2MM_w) = 0;
C=0;
}

*out = S;

}

При запуске с теми же X, Y и M это также возвращает тот же неверный результат, что и MWR2MM_CSA, несмотря на различные операции на уровне битов.

MWR2MM_cpa(X,Y,M) = 0x16C27CBC37C109B048B0F8B860C3501DB2E90F07D9BF9F6A63839453AC6603776C8CBD7AE8974544C52F078AD035AF1AC58CBBD5DB5801CDF3CF876C43F29FC1719ADF46804928D8BB621FCD48988160602C47812299603181FD97AEC74B7BE563EA0B0CB9EC9B2559191D8EE6AE8092FF9E50ADC1B874BC40C9256D785A4920DC1C1A5DF2B8492B181D16841EEA5377524BDF9BCC8A6DC3919DD4FDF6BBD7BB9D8FC35D06D7A4135363A2AA7FA6AE43B335A2704B007E405731A0D5D352EF7C51AD58241D201E07FA86AA395BB8F5AB3C9B966D5DB966777B45FE47B1838B97AFED23907D7AF61CF809D0B934FC3899998BFEF5B11516CA76C62D999CED8840

Для краткости я избавлю вас от двух других алгоритмов, которые также возвращают тот же неверный результат. Следует отметить, что оба этих алгоритма работают правильно при использовании с размером 4-битного операнда и размером 2-битного слова. Однако любые другие комбинации размера операнда / размера слова неверны, но имеют одинаковый неверный результат для всех четырех различных реализаций битового уровня.

Я не могу понять, почему все четыре алгоритма возвращают один и тот же неверный результат. Мой код в первом примере дословно идентичен алгоритму, предложенному в документе tenca-koc!

Я не прав, предполагая, что алгоритм MWR2MM должен возвращать тот же результат (в области Монтгомери), что и стандартный алгоритм MMX radix-2? Они имеют одинаковое основание, поэтому результаты должны быть одинаковыми, независимо от размера слова. Должен ли я не быть в состоянии обменять эти алгоритмы друг с другом?

извините за длинный пост, но я хочу быть очень точным и последовательным в объяснении, в чем проблема. Я не прошу помощи в отладке моего кода, скорее, пытаясь выяснить, неправильно ли я понимаю основную особенность алгоритмов умножения Монтгомери. Также любопытно, почему разные реализации дают одинаковые НЕПРАВИЛЬНО результат.

Спасибо!

0x116c27cbc37...
^