Безье — Расчет кривой по любым 3 точкам в нормализованной матрице с использованием переполнения стека
Если у меня есть простая двумерная матрица с нормализованными значениями на оси х от 0 до 1 и осями у от 0 до 1, и у меня есть 3 точки в этой матрице, например, P1 (x = 0,2, y = 0,9), P2 (x = 0,5, y = 0,1) и P3 (x = 0,9, y = 0,4).
Как я могу просто вычислить кривую по этим точкам, имея в виду функцию, которая дает мне y для любого x.
Я теперь, что есть любое количество возможных кривых через 3 точки. Но, эй, вы понимаете, что я имею в виду: мне нужна плавная кривая, пригодная для интерполяции аудиосэмплов, пригодная для вычисления кривой ослабления громкости, пригодная для расчета пути бега монстра в игре.
Сейчас я искал в сети этот вопрос около 3 дней, и я не могу поверить, что для этой задачи нет подходящего решения. Весь текст, касающийся Catmull-rom-Splines, кривых Безье и всех этих теоретических вещей, имеет как минимум одну точку, которая не делает его пригодным для меня. Например, сплайны Catmull-Rom должны иметь фиксированное расстояние между контрольными точками (я бы использовал этот код и установил 4. point-y в 3. point y):
void CatmullRomSpline(float *x,float *y,float x1,float y1,float x2,float y2,float x3,float y3,float x4,float y4,float u)
{
//x,y are calculated for x1,y1,x2,y2,x3,y3 and x4,y4 if u is the normalized distance (0-1) in relation to the distance between x2 and x3 for my whiched point
float u3,u2,f1,f2,f3,f4;
u3=u*u*u;
u2=u*u;
f1=-0.5f * u3 + u2 -0.5f *u;
f2= 1.5f * u3 -2.5f * u2+1.0f;
f3=-1.5f * u3 +2.0f * u2+0.5f*u;
f4=0.5f*u3-0.5f*u2;
*x=x1*f1+x2*f2+x3*f3+x4*f4;
*y=y1*f1+y2*f2+y3*f3+y4*f4;
}
Но я не вижу, чтобы x1-x4 оказали какое-либо влияние на вычисление y, поэтому я думаю, что x1-x4 должны иметь одинаковое расстояние?
…
Или код Безье не вычисляет кривую по точкам. Точки (по крайней мере, 2. точка), похоже, оказывают только силовое воздействие на линию.
typedef struct Point2D
{
double x;
double y;
} Point2D;
class bezier
{
std::vector<Point2D> points;
bezier();
void PushPoint2D( Point2D point );
Point2D GetPoint( double time );
~bezier();
};
void bezier::PushPoint2D(Point2D point)
{
points.push_back(point);
}
Point2D bezier::GetPoint( double x )
{
int i;
Point2D p;
p.x=0;
p.y=0;
if( points.size() == 1 ) return points[0];
if( points.size() == 0 ) return p;
bezier b;
for (i=0;i<(int)points.size()-1;i++)
{
p.x = ( points[i+1].x - points[i].x ) * x + points[i].x;
p.y = ( points[i+1].y - points[i].y ) * x + points[i].y;
if (points.size()<=2) return p;
b.PushPoint2D(p);
}
return b.GetPoint(x);
}
double GetLogicalYAtX(double x)
{
bezier bz;
Point2D p;
p.x=0.2;
p.y=0.9;
bz.PushPoint2D(p);
p.x=0.5;
p.y=0.1;
bz.PushPoint2D(p);
p.x=0.9;
p.y=0.4;
bz.PushPoint2D(p);
p=bz.GetPoint(x);
return p.y;
}
Это лучше, чем ничего, но это 1. очень медленно (рекурсивно) и 2. как я уже сказал, на самом деле 2. не вычисляет линию через 2. точку.
Есть ли математический мозг снаружи, который мог бы мне помочь?
Решение
Спасибо TOCS (Скотт) за предоставление вашего кода, я также попробую его, если у меня будет время. Но сейчас я проверил подсказку INFACT (ответ 3): эти «многочлены Ларгранжа» очень и очень близки к тому, что я ищу:
Я переименовал свой класс в кривую, потому что я добавил некоторый код для лагранжевой интерполяции. Я также добавил 3 картинки графического представления того, что код является расчетом.
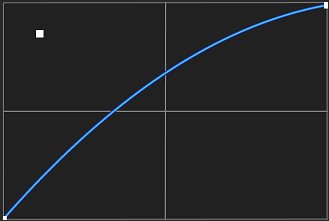
На рисунке 1 вы видите свободную среднюю точку старой функции Безье.
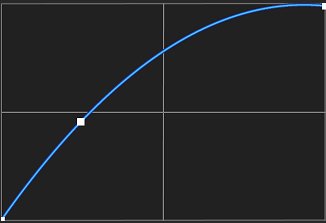
На рисунке 2 теперь вы можете видеть результат всех точек в результате интерполяции Лагранжа.
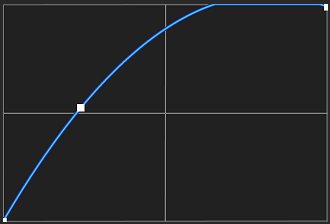
На рисунке 3 вы можете увидеть единственную проблему, или я должен сказать «вещь, которую мне также нужно решить» (в любом случае, это лучшее решение до сих пор): если я переместлю среднюю точку, кривая будет стремиться к быстрой, быстрой до верхней или нижней границы). Я бы хотел, чтобы он шел более плавно в верх и низ. Так что это выглядит как логарифм-функция. Так что он не выходит за границы y между 0 и 1 слишком рано.
Теперь мой код выглядит так:
curve::curve(void)
{
}
void curve::PushPoint2D(Point2D point)
{
points.push_back(point);
}
Point2D curve::GetPoint( double x )
{
//GetPoint y for x with bezier-mathematics...
//was the only calculating function in old class "bezier"//now the class is renamed "curve"int i;
Point2D p;
p.x=0;
p.y=0;
if( points.size() == 1 ) return points[0];
if( points.size() == 0 ) return p;
curve b;
for (i=0;i<(int)points.size()-1;i++)
{
p.x = ( points[i+1].x - points[i].x ) * x + points[i].x;
p.y = ( points[i+1].y - points[i].y ) * x + points[i].y;
if (points.size()<=2) return p;
b.PushPoint2D(p);
}
return b.GetPoint(x);
}
//THIS IS NEW AND VERY VERY COOL
double curve::LagrangeInterpolation(double x)
{
double y = 0;
for (int i = 0; i <= (int)points.size()-1; i++)
{
double numerator = 1;
double denominator = 1;
for (int c = 0; c <= (int)points.size()-1; c++)
{
if (c != i)
{
numerator *= (x - points[c].x);
denominator *= (points[i].x - points[c].x);
}
}
y += (points[i].y * (numerator / denominator));
}
return y;
}
curve::~curve(void)
{
}double GetLogicalYAtX(double x)
{
curve cv;
Point2D p;
p.x=0; //always left edge
p.y=y1; //now by var
cv.PushPoint2D(p);
p.x=x2; //now by var
p.y=y2; //now by var
cv.PushPoint2D(p);
p.x=1; //always right edge
p.y=y3; //now by var
cv.PushPoint2D(p);
//p=cv.GetPoint(x);
//return p.y;
return cv.LagrangeInterpolation(x);
}
У вас есть идеи, как я мог бы сделать новое решение немного более «мягким»? Так что я могу переместить 2. Точку в больших областях без кривой, выходящей за границы? Спасибо
Другие решения
static bezier From3Points(const Point2D &a, const Point2D &b, const Point2D &c)
{
bezier result;
result.PushPoint2D(a);
Point2D middle;
middle.x = 2*b.x - a.x/2 - c.x/2;
middle.y = 2*b.y - a.y/2 - c.y/2;
result.PushPoint2D(middle);
result.PushPoint2D(c);
return result;
}
Не проверено, но должно возвращаться кривая Безье, где при t = 0,5 кривая проходит через точку «b».
Кроме того (впереди еще больше непроверенного кода), вы можете рассчитывать свои очки, используя базовые полиномы Бернштейна.
static int binomialcoefficient (int n, int k)
{
if (k == 0)
return 1;
if (n == 0)
return 0;
int result = 0;
for (int i = 1; i <= k; ++i)
{
result += (n - (k - i))/i;
}
return result;
}
static double bernstein (int v, int n, double t)
{
return binomialcoefficient(v,n) * pow(t,v) * pow(1 - t,n - v);
}
Point2D GetPoint (double t)
{
Point2D result;
result.x = 0;
result.y = 0;
for (int i = 0; i < points.size(); ++i)
{
double coeff = bernstein (i,points.size(),t);
result.x += coeff * points[i].x;
result.y += coeff * points[i].y;
}
return result;
}
