Анализ главных компонентов с собственной библиотекой

Question

Анализ главных компонентов с собственной библиотекой

Я пытаюсь вычислить 2 основных компонента из набора данных в C ++ с помощью Eigen.

В настоящий момент я делаю это, чтобы нормализовать данные между [0, 1] а затем центрировать среднее. После этого я вычисляю ковариационную матрицу и запускаю на ней разложение по собственным значениям. Я знаю, что SVD работает быстрее, но я запутался в вычислительных компонентах.

Вот основной код о том, как я это делаю (где traindata моя входная матрица размером MxN):

Eigen::VectorXf normalize(Eigen::VectorXf vec) {
for (int i = 0; i < vec.size(); i++) { // normalize each feature.
vec[i] = (vec[i] - minCoeffs[i]) / scalingFactors[i];
}
return vec;
}

// Calculate normalization coefficients (globals of type Eigen::VectorXf).
maxCoeffs = traindata.colwise().maxCoeff();
minCoeffs = traindata.colwise().minCoeff();
scalingFactors = maxCoeffs - minCoeffs;

// For each datapoint.
for (int i = 0; i < traindata.rows(); i++) { // Normalize each datapoint.
traindata.row(i) = normalize(traindata.row(i));
}

// Mean centering data.
Eigen::VectorXf featureMeans = traindata.colwise().mean();
Eigen::MatrixXf centered = traindata.rowwise() - featureMeans;

// Compute the covariance matrix.
Eigen::MatrixXf cov = centered.adjoint() * centered;
cov = cov / (traindata.rows() - 1);

Eigen::SelfAdjointEigenSolver<Eigen::MatrixXf> eig(cov);
// Normalize eigenvalues to make them represent percentages.
Eigen::VectorXf normalizedEigenValues =  eig.eigenvalues() / eig.eigenvalues().sum();// Get the two major eigenvectors and omit the others.
Eigen::MatrixXf evecs = eig.eigenvectors();
Eigen::MatrixXf pcaTransform = evecs.rightCols(2);// Map the dataset in the new two dimensional space.
traindata = traindata * pcaTransform;

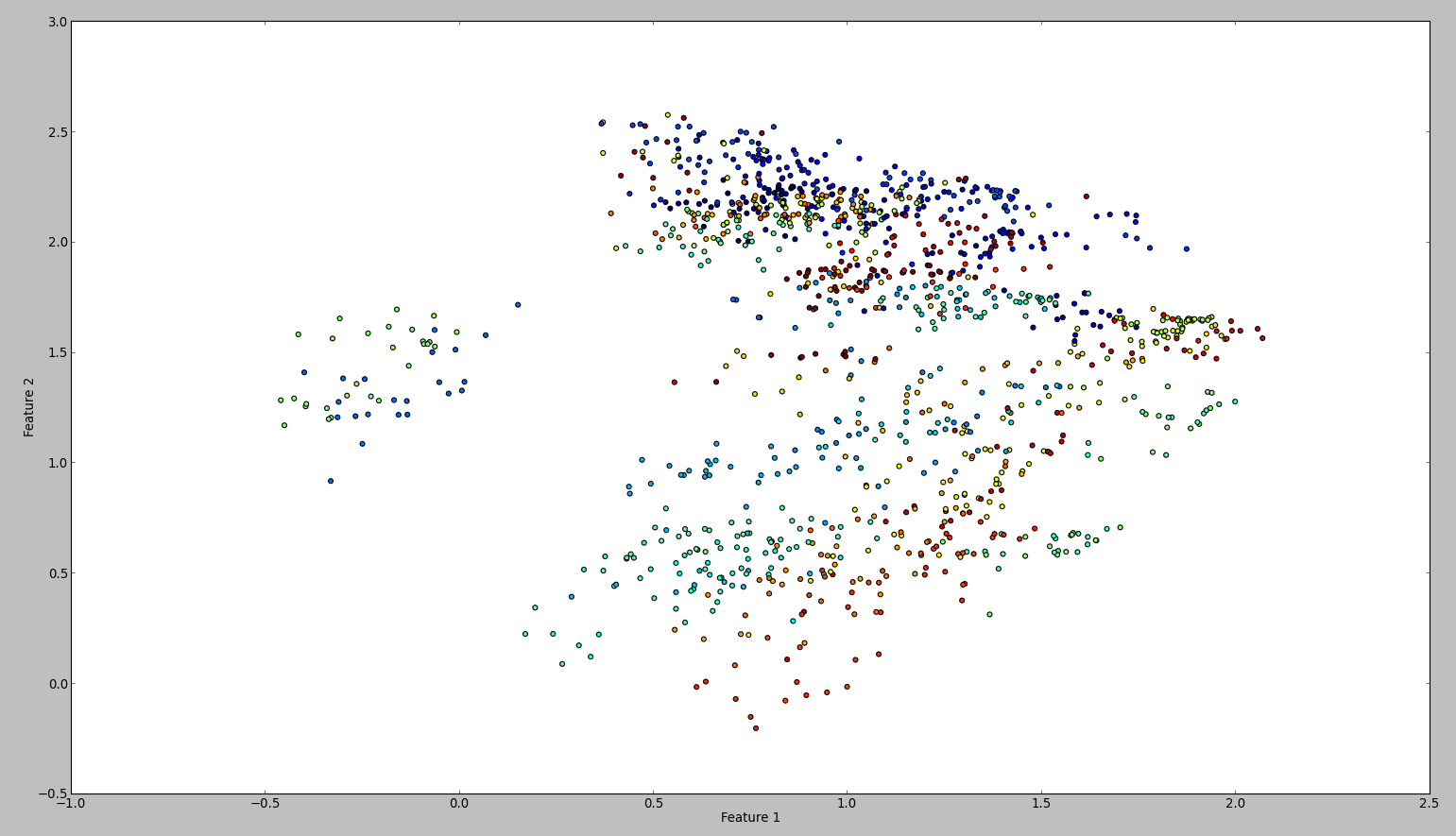
Результат этого кода выглядит примерно так:

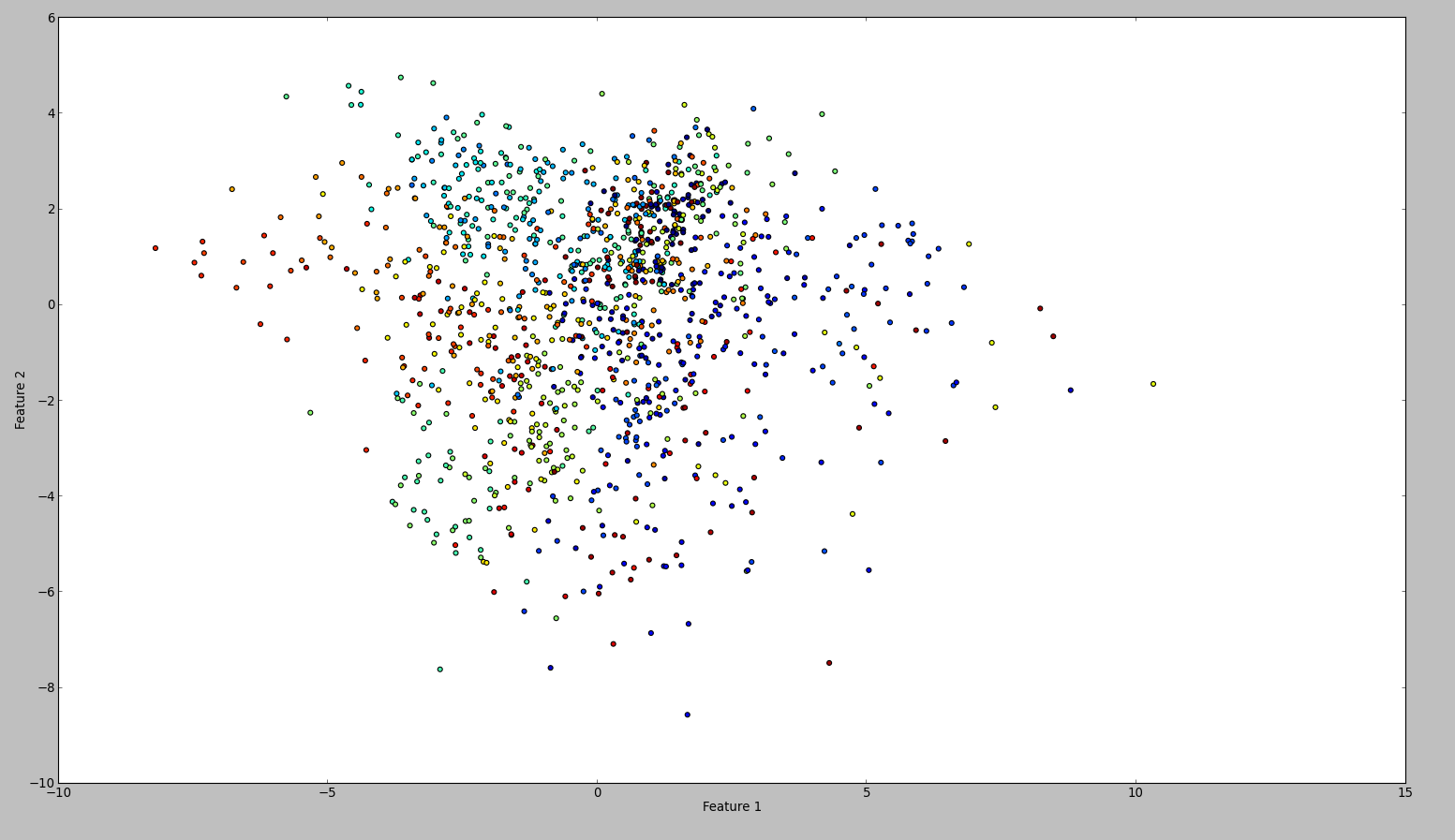
Чтобы подтвердить свои результаты, я попробовал то же самое с WEKA. Итак, я использовал нормализовать и центральный фильтр, в этом порядке. Затем основной компонент отфильтруйте и сохраните + построите график. Результат таков:

Технически я должен был сделать то же самое, однако результат был таким разным. Кто-нибудь может увидеть, если я сделал ошибку?

5

c++eigen pca

Решение

Другие решения

Причина была в том, что Weka нормированный набор данных. Это означает, что он масштабирует дисперсию каждого объекта до единичной дисперсии. Когда я это сделал, сюжеты выглядели одинаково. Технически мой подход тоже был правильным.

1

Источник

Accepted Answer

При масштабировании до 0,1 вы изменяете локальную переменную vec но забыл обновить traindata,

Более того, это можно сделать проще:

RowVectorXf minCoeffs = traindata.colwise().maxCoeff();
RowVectorXf minCoeffs = traindata.colwise().minCoeff();
RowVectorXf scalingFactors = maxCoeffs - minCoeffs;
traindata = (traindata.rowwise()-minCoeffs).array().rowwise() / scalingFactors.array();

то есть с использованием векторов строк и массив функции.

Позвольте мне также добавить, что симметричное разложение по собственным значениям на самом деле быстрее, чем SVD. Истинное преимущество SVD в этом случае состоит в том, что он избегает возведения в квадрат записей, но поскольку ваши входные данные нормализованы и центрированы, и что вы заботитесь только о самых больших собственных значениях, здесь нет проблем с точностью

4