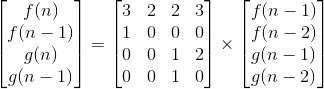алгоритм — Простое повторение в переполнении стека

Простой RecurrenceMax. Оценка 0

Наш герой — Алекс работает над исследованием в течение недели. И у него есть
недавно получил рекуррентное отношение для решения части этого
исследование. Но у него нет времени. Не могли бы вы сделать это?

Соотношение рекуррентности выглядит следующим образом: f (n) = 3 * f (n-1) + 2 * f (n-2) + 2
* g (n-1) +3 * g (n-2), g (n) = g (n-1) + 2 * g (n-2).

Вам дается начальное значение f (1), f (0), g (1), g (0).

Вы должны вывести f (N) mod 10 ^ 9.

Входные данные:

В первой строке вам даны 4 числа: f (1), f (0), g (1), g (0)
соответственно. В следующей строке вы получите целое число N.

Выход:

Выход f (N) мод 10 ^ 9.

Ограничения:

1 <= f (0), f (1), g (0), g (1) <= 10
1 <= N <= 10 ^ 18

Образец ввода (текстовая ссылка)

1 1 1 1
4
Пример вывода (текстовая ссылка)
162

Это действительно очень простой вопрос. Я просто использовал итерацию с 6 переменными f0, f1, f2, g0, g1, g2 для ее решения. В цикле я сначала вычисляю g2, f2, затем f0 = f1, f1 = f2, g0 = g1, g1 = g2. Типы данных без знака long long в c ++.

Тем не менее, ограничение по времени составляет 1 секунду, и я получаю 1,06 секунды. Поэтому в тесте я прошел только один тестовый пример, другие «превышен лимит времени». Есть ли более быстрый способ решить это?

мой код:

#include<iostream>
using namespace sdt;

int main()
{
unsigned long long f0, f1, g0, g1, f2, g2;
unsigned long long N;
cin>>f1>>f0>>g1>>g0;
cin>>N;
for(unsigned long long i=2; i<N+1; i++)
{
f2=3*f1+2*f0+2*g1*3*g0;
g2=g1+2*g0;
f0=f1;
f1=f2;
g0=g1;
g1=g2;
}
unsigned long long result=f2%1000000000;
cout<<result;
return 0;
}