алгоритм — Нахождение кривизны из зашумленного набора точек данных, используя 2d / 3dsplines? (C ++)

Я пытаюсь извлечь кривизну импульса вдоль его профиля (см. Рисунок ниже). Импульс рассчитывается по сетке длины и высоты: 150 х 100 ячеек с использованием метода конечных разностей, реализованного в C ++.

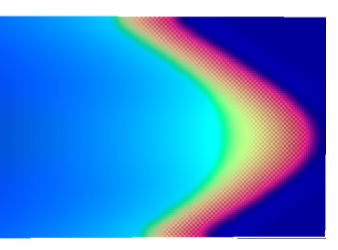
Я извлек все точки с одинаковым значением (контур / уровень) и пометил их красной непрерывной линией на рисунке ниже. Другие цвета незначительны.

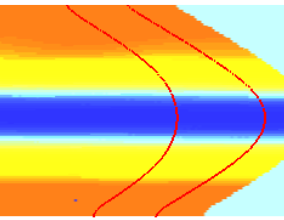
Затем я попытался найти кривизну по этой уже зашумленной (из-за дискретности сетки) контурной линии следующими способами:

(скользящее среднее уже применено)

1) Кривизна через касательные

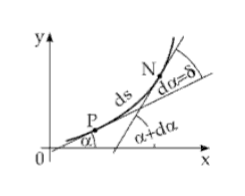
Кривизна линии в точке P определяется как:

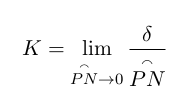
Таким образом, кривизна представляет собой кривые дельты угла по длине дуги между P и N. Поскольку мои точки имеют определенное расстояние между ними, я не смог бы достаточно приблизить изгибы, чтобы кривизна не была рассчитана правильно. Я проверил это с помощью круга, который, естественно, имеет постоянную кривизну. Но я не мог воспроизвести это (только 1 значащая цифра была правильной).

2) Вторая производная линии, параметризованная по длине дуги

Я рассчитал первую производную линии по длине дуги, сглаженную с помощью скользящего среднего, а затем снова взял производную (2-я производная). Но здесь я также получил только 1 значащую правильную цифру.
К сожалению, взятие производной умножает уже свойственный шум на более высокие уровни.

3) Локальное приближение линии кружком

Поскольку обратная величина радиуса окружности является кривизной, я использовал следующий подход:

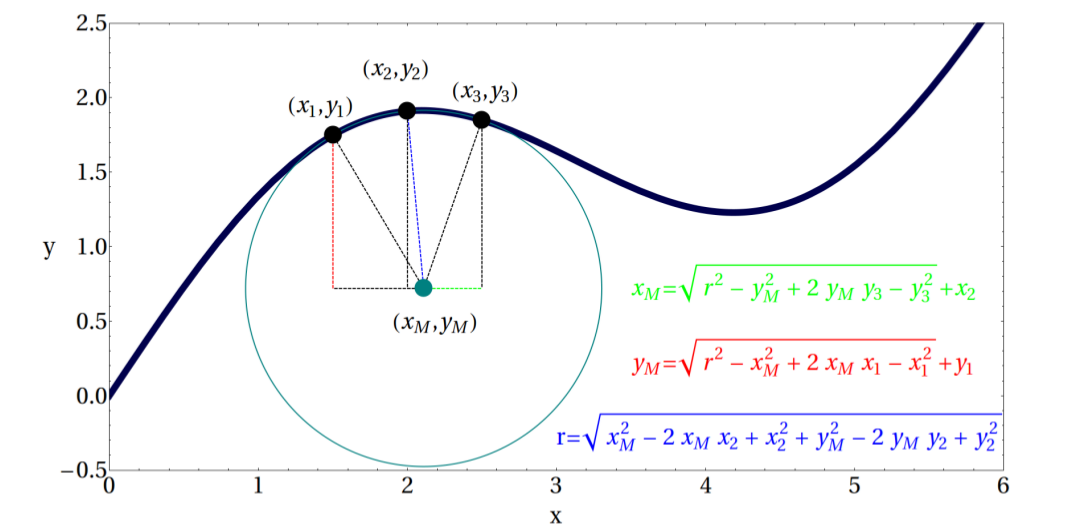
Это сработало лучше всего (2 правильные значащие цифры), но мне нужно уточнить еще дальше. Итак, моя новая идея заключается в следующем:

Вместо того чтобы использовать значения в дискретных точках для определения кривизны, я хочу аппроксимировать профиль импульса с помощью трехмерной поверхности сплайна. Затем я извлекаю из него набор уровней определенного значения, чтобы получить плавную линию точек, из которой я могу найти хорошую кривизну.

До сих пор я не мог найти библиотеку C ++, которая может генерировать такую ​​поверхность сплайна Безье. Не могли бы вы указать мне на кого-нибудь?

Кроме того, вы думаете, что этот подход стоит попробовать, или я потеряю слишком много точности в своей кривизне?

Знаете ли вы какой-либо другой подход?

С наилучшими пожеланиями,
январь

редактировать: кажется, что я не могу публиковать фотографии как новый пользователь, поэтому я удалил их все из своего вопроса, хотя я считаю, что они важны для объяснения моей проблемы. Есть ли способ, которым я все еще могу показать их?

edit2: хорошо, готово 🙂