Алгоритм минимального расстояния в R

Я написал функцию в C ++, которая делает следующее: учитывая (возможно, очень длинный) вектор x и порог thrнайти подпоследовательность y из x такой, что x[1]∈y, x[length(x)]∈y, а также ∀i∈1:length(y) y[i+1]-y[i]≥thr, Намерение состоит в том, чтобы найти короткую последовательность x где plot(x) «выглядит так же», как plot(x[subsequence])в том смысле, что разрешение графа thr,

Функция является частью пакета R, используя Rcpp интерфейс для вызова функций C ++. Источник здесь: https://gist.github.com/kenahoo/8922376 . (Это на самом деле работает на data.frameне простой вектор, но это эквивалентно работе с каждым столбцом независимо как вектор, а затем слияние последовательностей индекса.)

Я хотел бы найти эквивалентное решение чистого R, которое приятно & эффективный — одна очевидная идея что-то вроде which(diff(x)>thr), но это не уместно, потому что он пропустит любые медленные изменения в значениях, которые накапливаются с течением времени до более чем thr,

Пример:

> set.seed(123)
> x <- cumsum(runif(100, -1, 1))
> y <- downsampleForPlot(data.frame(x=x), 2.5)
> y
[1]   1  11  26  46  57  71  81 100

Это производит приближение как это:

> plot(x)
> lines(stepfun(y[-1], x[y], f=0), col='blue')

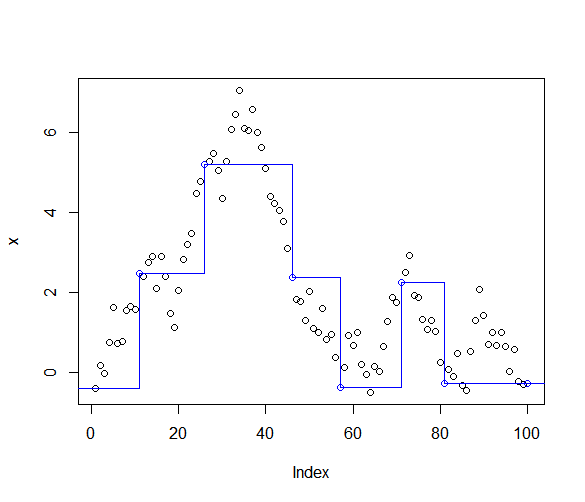
Любые идеи для этого приветствуются.