Алгоритм Флойда Варшалла для плоского графа сетки
У меня есть такой график:
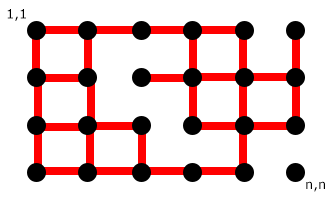
И я реализовал граф массив, как это:
G[i][j][k]
Kимеет только 4 ячейки и показывает, связана ли вершина с четырьмя соседними вершинами или нет. Например для:
G[1][1][0] = 0
G[1][1][1] = 1
G[1][1][2] = 1
G[1][1][3] = 0
Это показывает, что вершина (1, 1) связана с 2 вершинами.
Я знаю алгоритм Флойда Варшалла для нормальных типов графиков. Но как я могу реализовать алгоритм Flyod Warshall для такого рода графиков?
Поблагодарить.
Решение
Алгоритм Флойда-Варшалла был бы очень неэффективным для такого разреженного графа. Граф разрежен, потому что каждая вершина соединена не более чем с 4 другими вершинами. В плотном графе вершина может быть соединена с N-1 другими вершинами, где N — количество вершин в графе. Вот где алгоритм Флойда-Варшалла будет более или менее эффективным, но, тем не менее, если вам не нужны кратчайшие пути между каждой парой вершин или поиск циклов отрицательной длины, рассмотрите возможность использования очереди приоритетов для нахождения кратчайшего пути между источником и все остальные вершины: https://en.wikipedia.org/wiki/Dijkstra’s_algorithm#Using_a_priority_queue . Или даже поиск в ширину может использоваться, если веса на вашем графике равны для каждого ребра (невзвешенный график).
Если вам все еще нужен алгоритм Флойда-Варшалла для вашей сетки, вот он. Рассмотрим сетку N от Mс индексированием на основе 1, так что максимальная запись в сетке G[N][M][...], Тогда алгоритм Флойда-Варшалла будет:
// edge offsets
const int offs[4][2] = {
{-1, 0}, {0, 1}, {1, 0}, {0, -1}
};
const int INF_DIST = 1e9;
int D[N+1][M+1][N+1][M+1];
//// Initialize weights to infinity
// For each source row and column (i,j)
for(int i=1; i<=N; i++) {
for(int j=1; j<=M; j++) {
// For each destination row and column (k,l)
for(int k=1; k<=N; k++) {
for(int l=1; l<=M; l++) {
D[i][j][k][l] = INF_DIST;
}
}
}
}
//// Mark edges of the graph
// For each row
for(int i=1; i<=N; i++) {
// For each column
for(int j=1; j<=M; j++) {
// For each of the directions: up(k=0), right(k=1), down(k=2) and left(k=3)
for(int k=0; k<=3; k++) {
if(G[i][j][k] == 0) {
// Don't add this edge to the distance matrix
// if the edge is not in the grid graph
continue;
}
// Calculate (r, c) as the coordinates of the vertex one step
// in the direction k
int r = i + offs[k][0];
int c = j + offs[k][1];
if(1<=r && r <= N && 1<=c && c<=M) {
// Only add the edge (if exists) in case (r, c) is within the grid
D[i][j][r][c] = G[i][j][k];
}
}
}
}
//// Find shortest paths between each pair of vertices
// For each intermediate vertex (k,l)
for(k=1; k<=N; k++) {
for(l=1; l<=M; l++) {
// For each source vertex (i,j)
for(int i=1; i<=N; i++) {
for(int j=1; j<=M; j++) {
// For each destination vertex (r,c)
for(int r=1; r<=N; r++) {
for(int c=1; c<=M; c++) {
// Apply the triangle rule
int alternative = D[i][j][k][l] + D[k][l][r][c];
if(alternative < D[i][j][r][c]) {
D[i][j][r][c] = alternative;
}
}
}
}
}
}
}
Другие решения
Ваше графическое представление в основном список смежности, для каждой вершины v= G[i][j], у вас есть список, содержащий ребра, с которыми связан граф. В вашем случае список состоит из 4 логических значений — каждое указывает на то, (i,j) связан с (i-1,j),(i+1,j),(i,j-1),(i,j+1)Таким образом, использование алгоритма Флойд-Варшалла с таким пониманием довольно просто, если смотреть на Википедия псевдокод:
1 let dist be a |V| × |V| array of minimum distances initialized to ∞ (infinity)
2 for each vertex v
3 dist[v][v] ← 0
4 for each edge (u,v)
5 dist[u][v] ← w(u,v) // the weight of the edge (u,v)
6 for k from 1 to |V|
7 for i from 1 to |V|
8 for j from 1 to |V|
9 if dist[i][j] > dist[i][k] + dist[k][j]
10 dist[i][j] ← dist[i][k] + dist[k][j]
11 end if
Основное отличие заключается в строках 4-5, где:
for each edge(u,v):
на самом деле
for each x=0,1,...,n-1
for each y=0,1,...,m-1
for each i=0,1,2,3:
//if G[x][y][y] == 1 : it's an edge
Также обратите внимание, что в вашем графике максимальный коэффициент ветвления (количество ребер, соединенных с узлом) равен 4. Это означает, что максимальное число ребер в графе равно |E| <= 4|V|,
Поскольку ваш график не направлен, поиск кратчайшего пути для всех можно сделать более эффективно, выполнив BFS от каждого узла, это займет O(|V|*(|E|+|V|)) время, но так как |E| <= 4|V|, это O(|V|^2) — по сравнению с Флойд-Варшалл, который работает в O(|V|^3),
