алгоритм — C ++ Полиномиальное распределение

Я пытаюсь закодировать полиномиальный алгоритм, который будет в основном применять биномиальное распределение к каждому значению входного вектора, зная значения всех предыдущих. Это направлено здесь на создать новую популяцию для нескольких аллелей зная начальную популяцию.

Чтобы добиться этого, я использую этот рекурсивный алгоритм:

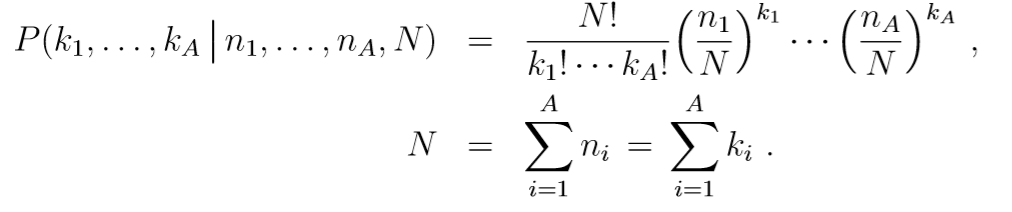
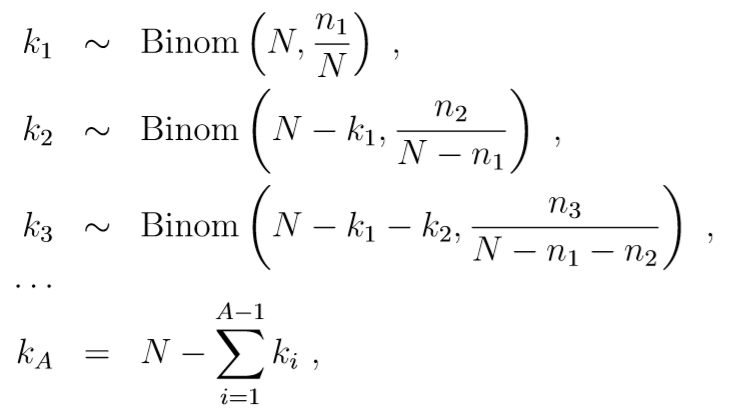
Вот как выглядит мой код прямо сейчас:

void RandomNumbers::multinomial(std::vector<unsigned int>& alleleNumbers) {

/*  In this function we need two different records of the size.
*  We need the size from the old populations, ( N - n1 - ... - nA )
*  and we also need the size from the newly created population,
*  ( N - k1 - ... - kA ).
*  In order to achieve such a task, we'll use the integer "temp" to store
*  the value n1 before modifying it to k1 and so on.
*
*
*/
double totalSize = 0;

for(auto n : alleleNumbers) totalSize+=n;

double newTotalSize(totalSize);

std::cout<< newTotalSize;

for(size_t i = 0; i < alleleNumbers.size(); ++i){
size_t temp = alleleNumbers[i];
alleleNumbers[i] = binomial(newTotalSize,
(alleleNumbers[i])/(totalSize));
newTotalSize-= alleleNumbers[i];
totalSize = temp;
}
}

Но я совсем не уверен в этом, и мне было интересно, существует ли уже существующий многочленный алгоритм такого рода …

Большое спасибо.