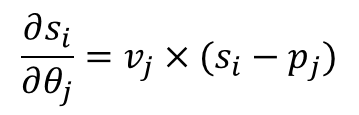5 DOF Обратная кинематика для якобиевых матриц

Я пытаюсь применить IK к руке моего человеческого скелета, где положение плеча зафиксировано, и движется только рука.

FK руки выглядит следующим образом

(x,y,z) = Root_T * Shoulder_T * Shoulder_Rx(q_0) * Shoulder_Ry(q_1) *
Shoulder_Rz(q_2) * Elbow_T * Elbow_Rx(q_3) * Hand_T * Hand_Rx(q_4) * Position

Это моя ИК решающая функция

//Q_desired is a 5*1 Vector whose entries are initialized as 0.0
//TargetP is where I want the end effector to be
void BoneRig::solveIK(glm::vec3& targetP, Eigen::VectorXf& Q_desired) {
//Basic setups
float error = 10.0f;
glm::vec3 errorP;
Eigen::VectorXf deltaQ(5);
glm::vec3 endEffector = glm::vec3(0.0f,0.0f,0.0f);
Eigen::MatrixXf J(3,5);
Eigen::MatrixXf J_plus(5,3);
float deltaTime = 0.1;

int limit = 1000;
int limitCounter = 0;

while(error > 0.01){
//gets the current endEffector location and stores it in endEffector
getEndEffectorP(endEffector);
errorP = targetP - endEffector;

Eigen::VectorXf deltaX(3);
deltaX << (errorP * deltaTime).x, (errorP * deltaTime).y, (errorP * deltaTime).z;

getJacobian(J, targetP);
J_plus = J.transpose();
deltaQ = J_plus * deltaX;

Q_desired += deltaQ;
setOrientation(Q_desired);

error = glm::length(errorP);

if(limitCounter>= limit){
std::cout << "You could not solve this"<<std::endl;
break;
}
}
}

Я думаю, что проблема в setOrientation(Q_desired); функция. Q_desired = Q_desired + deltaQ обновляет углы DOF в каждом цикле, поэтому я соответствующим образом обновляю матрицы вращения каждого соединения. Здесь setOrientation(Q_desired) функция.

//Joints[15] is the Shoulder joint, Joints[16] is the Elbow joint.
//Joints[17] is the Hand joint
void BoneRig::setOrientation(const Eigen::VectorXf& ceta_d){
glm::mat4 temp = glm::mat4(1.0f);
Joints[15].setR(glm::rotate(temp,ceta_d(0),glm::vec3(1.0f,0.0f,0.0f)));
Joints[15].setR(glm::rotate(Joints[15].returnR(),ceta_d(1),glm::vec3(0.0f,1.0f,0.0f)));
Joints[15].setR(glm::rotate(Joints[15].returnR(),ceta_d(2),glm::vec3(0.0f,0.0f,1.0f)));
temp = glm::mat4(1.0f);
Joints[16].setR(glm::rotate(temp,ceta_d(3),glm::vec3(1.0f, 0.0f, 0.0f)));
temp = glm::mat4(1.0f);
Joints[17].setR(glm::rotate(temp,ceta_d(4),glm::vec3(1.0f, 0.0f, 0.0f)));
return;
}

Мне было любопытно, следует ли применять угол поворота по этой оси вращения (должна ли это быть глобальная ось, а не локальная ось?). Я не опубликовал метод getJacobian (), потому что я думаю, что это правильно, но я сделаю, если в этом коде нет недостатка. Любая помощь будет оценена. Заранее спасибо!

РЕДАКТИРОВАТЬ
Так я получаю матрицу Якоби для руки. Обратите внимание, что только плечо является шарнирным и гнездовым соединением, а остальные — просто вращающиеся соединения, основанные на локальной оси X.

void BoneRig::getJacobian(Eigen::MatrixXf& J, glm::vec3& targetWorld){
glm::vec4 xAxis = glm::vec4(1.0f,0.0f,0.0f,0.0f);
glm::vec4 yAxis = glm::vec4(0.0f,1.0f,0.0f,0.0f);
glm::vec4 zAxis = glm::vec4(0.0f,0.0f,1.0f,0.0f);
glm::mat4 temp = Joints[0].returnT() * Joints[0].returnR() * Joints[11].returnT() * Joints[11].returnR() * Joints[14].returnT() * Joints[14].returnR() * Joints[15].returnT() * Joints[15].returnR();
glm::vec3 worldXAxis = glm::vec3(temp * xAxis);
glm::vec3 worldYAxis = glm::vec3(temp * yAxis);
glm::vec3 worldZAxis = glm::vec3(temp * zAxis);
glm::vec3 worldPos = glm::vec3(temp * glm::vec4(0.0f,0.0f,0.0f, 1.0f));
glm::vec3 p = targetWorld - worldPos;

glm::vec3 upperPart = glm::cross(worldXAxis,p);
J(0,0) = upperPart.x;
J(1,0) = upperPart.y;
J(2,0) = upperPart.z;

upperPart = glm::cross(worldYAxis,p);
J(0,1) = upperPart.x;
J(1,1) = upperPart.y;
J(2,1) = upperPart.z;

upperPart = glm::cross(worldZAxis,p);
J(0,2) = upperPart.x;
J(1,2) = upperPart.y;
J(2,2) = upperPart.z;

temp = temp * Joints[16].returnT() * Joints[16].returnR();
worldXAxis = glm::vec3(temp * xAxis);
worldPos = glm::vec3(temp * glm::vec4(0.0f,0.0f,0.0f, 1.0f));
p = targetWorld - worldPos;
upperPart = glm::cross(worldXAxis,p);
J(0,3) = upperPart.x;
J(1,3) = upperPart.y;
J(2,3) = upperPart.z;
temp = temp * Joints[17].returnT() * Joints[17].returnR();

worldXAxis = glm::vec3(temp * xAxis);

worldPos = glm::vec3(temp * glm::vec4(0.0f,0.0f,0.0f, 1.0f));

p = targetWorld - worldPos;
upperPart = glm::cross(worldXAxis,p);

J(0,4) = upperPart.x;
J(1,4) = upperPart.y;
J(2,4) = upperPart.z;
}

Я использовал это уравнение для каждого столбца матрицы Якоби. Ось должна быть рассчитана в глобальных координатах, вот что я сделал в коде.