3D-объект вращается вдоль всех трех осей, когда требуется только вращение по оси X

Поэтому я реализую вращения для своих 3D-объектов в сцене OpenGL, и пока сами основные вращения (с использованием кватернионов) работают нормально. Я также в основном решил проблему «наблюдения», так что теперь я могу заставить любой трехмерный объект, включая камеру, точно и без затруднений смотреть на любую точку в трехмерном пространстве.

тем не мение, когда команда указывает объекту на заданную точку, он часто катится вдоль своей локальной оси Z; посмотрите на это изображение, где маленький корабль смотрит в точку, где сходятся красные, зеленые и синие линии. Вы можете видеть, как он выглядит не так, как можно было бы ожидать от объекта, который, скажем, вращался вдоль своей оси Y в направлении зеленой линии, а затем наклонялся вдоль своей оси X в направлении точки встречи трех линий.

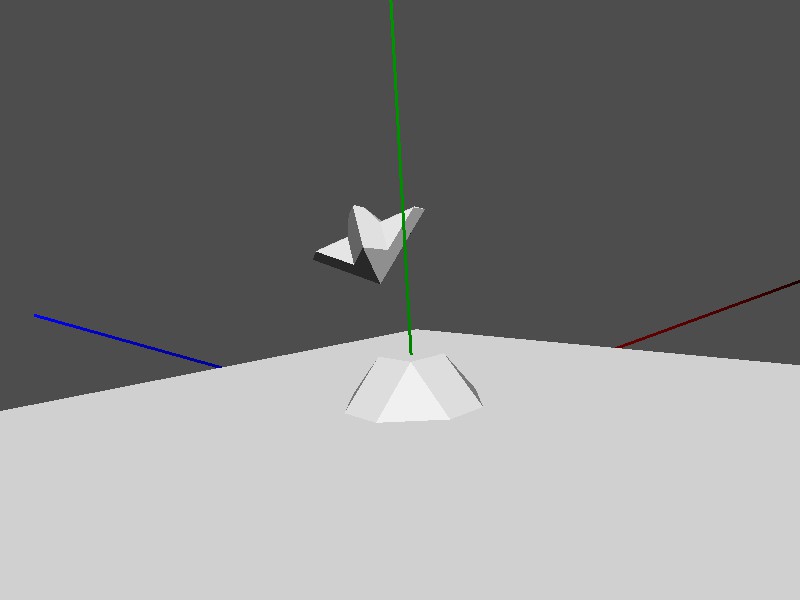
Я не обязательно этого хочу. Я бы предпочел, чтобы он смотрел прямо на эту точку, но наклонился бы немного дальше по часовой стрелке (если смотреть спереди), так что кончики его крыльев находятся на том же уровне Y. Поскольку вся точка столкновения с точкой состоит в том, что локальная ось Z проходит через эту точку, не должно иметь значения, как объект вращается вокруг своей локальной оси Z, однако результирующее вращение постоянно отклоняется, хотя перекос, кажется, зависит от относительное положение объекта и его точка фокуса.

В любом случае, вот мой код LookAt (), который я хотел бы изменить так, чтобы у меня был больший контроль над окончательным вращением Z.

void Thing::LookAt(sf::Vector3<float> Target)
{
///Derived from pseudocode found here:
///http://stackoverflow.com/questions/13014973/quaternion-rotate-to
//Reset the rotation to default
m_Orientation = Quaternion();

//Get the normalized vector from the camera position to Target
sf::Vector3<double> VectorTo(Target.x - m_Position.x,
Target.y - m_Position.y,
Target.z - m_Position.z);
//Get the length of VectorTo
double VectorLength = sqrt(VectorTo.x*VectorTo.x +
VectorTo.y*VectorTo.y +
VectorTo.z*VectorTo.z);
//Normalize VectorTo
VectorTo.x /= VectorLength;
VectorTo.y /= VectorLength;
VectorTo.z /= VectorLength;

//Straight-ahead vector
sf::Vector3<double> LocalVector = m_Orientation.MultVect(sf::Vector3<double>(0, 0, -1));

//Get the cross product as the axis of rotation
sf::Vector3<double> Axis(VectorTo.y*LocalVector.z - VectorTo.z*LocalVector.y,
VectorTo.z*LocalVector.x - VectorTo.x*LocalVector.z,
VectorTo.x*LocalVector.y - VectorTo.y*LocalVector.x);
//Normalize the axis
//Get the length of VectorTo
double AxisLength = sqrt(Axis.x*Axis.x +
Axis.y*Axis.y +
Axis.z*Axis.z);
//Normalize VectorTo
Axis.x /= AxisLength;
Axis.y /= AxisLength;
Axis.z /= AxisLength;

//Get the dot product to find the angle
double DotProduct = (VectorTo.x*LocalVector.x +
VectorTo.y*LocalVector.y +
VectorTo.z*LocalVector.z);
double Angle = acos(DotProduct);

//Determine whether or not the angle is positive
//Get the cross product of the axis and the local vector
sf::Vector3<double> ThirdVect(Axis.y*LocalVector.z - Axis.z*LocalVector.y,
Axis.z*LocalVector.x - Axis.x*LocalVector.z,
Axis.x*LocalVector.y - Axis.y*LocalVector.x);
//If the dot product of that and the local vector is negative, so is the angle
if (ThirdVect.x*VectorTo.x + ThirdVect.y*VectorTo.y + ThirdVect.z*VectorTo.z < 0)
{
Angle = -Angle;
}

//Finally, create a quaternion
//Quaternion AxisAngle;
m_Orientation.FromAxisAngle(Angle, Axis.x, Axis.y, Axis.z);
m_Orientation.RotationMatrix(m_RotationMatrix);
}

Моя проблема в том, что я не знаю, как мне получить контроль над окончательным вращением вокруг оси Z. Обратите внимание, что когда я извлекаю угол Z из кватерниона m_Orientation, он говорит мне, что изображенный выше корабль вращается на 0 радиан вокруг своей оси Z. Я попытался вручную установить для компонента Z значение 0 и перенормировать кватернион, но (очевидно, я полагаю) это не сработало.

В настоящее время было бы хорошо рассчитать конкретный Z-компонент, необходимый для поворота корабля «вверх тормашками», то есть так, чтобы два его кончика крыла находились на одном уровне Y, а его ось Y была как можно более крутой, но Я хотел бы получить более четкое представление о том, как манипулировать окончательным вращением Z. Есть идеи или ресурсы?